Выпуклость и вогнутость кривых. Точки перегиба
График функции y=f(x) называется выпуклым (вогнутым) в интервале (а, в), если точки кривой расположены ниже (выше) касательной, проведенной в любой ее точке этого интервала.
Точка, отделяющая выпуклую часть графика функции от вогнутой части, называется точкой перегиба. Теорема 1. Если во всех точках интервала (а, в) вторая производная функции f(x) отрицательна, т.е. f" (x) Следовательно, точки перегиба функции y=f(x) следует искать среди точек, в которых либо f" (x)=0, либо f" (x)=∞. Теорема 2. Пусть для функции y=f(x) ее вторая производная f" (x) существует в некоторой окрестности точки Пример. Найти интервалы выпуклости и вогнутости и точки перегиба графика функции.
Решение. Область определения функции – вся числовая ось: (-∞; ∞). Находим производные: y’=
Решим уравнение: Исследуем знаки
В интервалах Точки
А(-2; -124) и В( Решить самостоятельно. Для данных функций найти a) интервалы монотонности и экстремумы и b) интервалы выпуклости, вогнутости и точки перегиба: 1) 4) 6.7. Наибольшее и наименьшее значения функции на отрезке. Если функция y=f(x) непрерывна на отрезке Чтобы найти наибольшее и наименьшее значения функции y=f(x) на отрезке Пример. Наибольшее и наименьшее значения функции Решение.
Находим значение функции на концах отрезка:
Из трех полученных значений выбираем самое большое и самое меньшее:
Решить самостоятельно. Найти наибольшее и наименьшее значения функции на заданном отрезке: 1) 3)
|


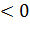 , то кривая y=f(x) в этом интервале выпуклая. Если же во всех точках интервала (а, в) f" (x)> 0, то кривая в этом интервале вогнутая.
, то кривая y=f(x) в этом интервале выпуклая. Если же во всех точках интервала (а, в) f" (x)> 0, то кривая в этом интервале вогнутая. за исключением, быть может, самой точки
за исключением, быть может, самой точки 


 , т.е.
, т.е. 
 :
:




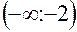 и
и 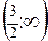 f" (x)> 0 следовательно в этих интервалах кривая вогнута, в интервале
f" (x)> 0 следовательно в этих интервалах кривая вогнута, в интервале 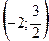 f" (x)< 0=> в этом интервале кривая выпуклая.
f" (x)< 0=> в этом интервале кривая выпуклая.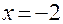 и
и  - точки перегиба, их координаты
- точки перегиба, их координаты
 т.е.
т.е. - точки перегиба.
- точки перегиба. 2)
2)  3)
3) 
 5)
5)  6)
6) 
 , то она достигает на нем своего наибольшего и наименьшего значений (теорема Вейерштрасса). Эти значения достигаются функцией либо в точках экстремума, находящихся внутри отрезка, либо на его концах.
, то она достигает на нем своего наибольшего и наименьшего значений (теорема Вейерштрасса). Эти значения достигаются функцией либо в точках экстремума, находящихся внутри отрезка, либо на его концах. на отрезке
на отрезке 
 . Находим критические точки:
. Находим критические точки:
 . Точка
. Точка  не принадлежит отрезку
не принадлежит отрезку 
 ;
; 
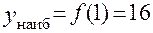

 2)
2) 

 ;
;  4)
4) 




