Интегрирование путем замены переменной
(или способом подстановки) Этот способ заключается во введении новой переменной интегрирована. При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Пусть требуется найти
После нахождения интеграла в правой части этого равенства следует перейти от новой переменной t к переменной x. При интегрировании иногда целесообразно подбирать замену переменной не в виде x=y(t), а в виде y(x)=t. Рассмотрим примеры: 1)
2) 3)
4)
5) 7.3. Интегрирование по частям: Пусть u и v – две дифференцированные функции от X. Имеет место формула: При применении метода интегрирования по частям подынтегральное выражение данного интеграла развивают на два множителя u и dv, затем находя du (дифференцируя u) и v (интегрируя dv) и применяют указанную выше формулу, сводя вычисление интеграла С помощью интегрирования по частям берутся интегралы следующих типов: Рассмотрим примеры:
1) 2) 3) 4) 7.4. Интегрирование функций, содержащих в значителе квадратный трехчлен:
Рассмотрим первые два интеграла, чтобы их вычислить квадратный трехчлен, стоящий в значителе, надо дополнить до полного квадрата. В результате исходный интеграл сводится к виду:
1. 2. 3.
4 Интегралы вида 1) Вычислителем дроби вычисляется выражение, являющееся производной квадратного трехчлена, стоящего в значителе; 2) Исходный интеграл развивается на сумму двух интегралов путем деления на данный знаменатель, причем числителем первой дроби является производная квадратного трехчлена, а второй – оставшееся число; 3) Вычисляем два интеграла, которые являются табличными.
Рассмотрим примеры: 5)
6)
|

 . сделаем подстановку x=y(t), где y(t) – функция, имеющая непрерывную производную. Тогда dx=y’(t)dt и получаем формулу интегрирования подстановкой:
. сделаем подстановку x=y(t), где y(t) – функция, имеющая непрерывную производную. Тогда dx=y’(t)dt и получаем формулу интегрирования подстановкой:
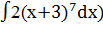 сделаем подстановку 2x+3=t, тогда dt=2dx dx=dt/2 имеем
сделаем подстановку 2x+3=t, тогда dt=2dx dx=dt/2 имеем +C
+C =
= 
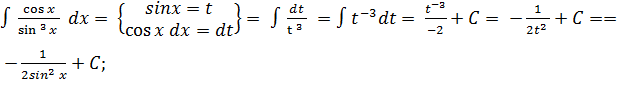

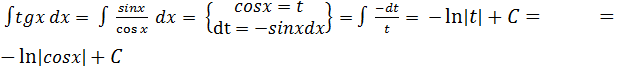

 к вычислению интеграла
к вычислению интеграла  . Этот метод целесообразно применять, когда последний интеграл проще исходного.
. Этот метод целесообразно применять, когда последний интеграл проще исходного.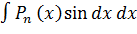 ,
, 
 , (в качестве «u» берут многочлен Рn(x), а остальное принимают за dv),
, (в качестве «u» берут многочлен Рn(x), а остальное принимают за dv),  ,
, 
 , (принимают dv= Рn(x)dx а остальное принимают за u).
, (принимают dv= Рn(x)dx а остальное принимают за u). (3x+1) sin 2x -
(3x+1) sin 2x - 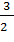 (-
(- 

 +C
+C

 или
или  либо
либо 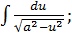 а эти интегралы являются табличными. Рассмотрим примеры:
а эти интегралы являются табличными. Рассмотрим примеры: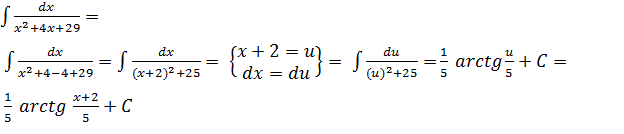
 =
= 


 вычисляются по следующей схеме:
вычисляются по следующей схеме: +C
+C



