Свойства определенного интеграла. 1) Если существует то существует причем
1) Если существует
2) 3) 4) Если 5) Если m и M – наименьшее и наибольшее значения f(x) на отрезке [a, b], то M(b-a) 6) Если f(x) непрерывна на отрезке [a, b], то на этом отрезке найдется такая точка ξ, что 7) Для любой трех чисел a, b, c справедливо равенство:
8.3. Вычисление определенного интеграла:
Имеет место формула Ньютона Лейбница:
1)
2)
3) 8.4. Замена переменной в определенном интеграле:
Пусть дан интеграл Введем новую переменную t по формуле x=y(t) Если 1) y(α) = a; y(β) = b, 2) y(t) = y’(t) – непрерывны на [α, ρ ] 3) f(y(t)) определена и непрерывна на [α, ρ ], то
При вычислении определенного интеграла по этой формуле не надо возвращаться к старой переменной Пример1
Положим: x-1 = t2 х=t2 -1; dx = 2tdt Если x=1, то 1-1 = α 2; Если x=5, то 5-1 = β 2;
Пример 2
= 8.5. Интегрирование по частям:
Пусть U и V- дифференцируемые функции от x. (UV)’ = U’V+UV’откуда следует
Но
Пример 1
Пример 2
|

 то существует
то существует 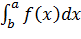 причем
причем

 =
= 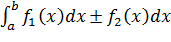
 x
x  [a, b], то
[a, b], то 



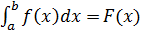 | a/b= F(b)-F(a), где F(x) – первообразная от f(x).
| a/b= F(b)-F(a), где F(x) – первообразная от f(x). =
= 
 = 2(
= 2( )=2(2-1)=2
)=2(2-1)=2
 = ½ ln8/5
= ½ ln8/5
 =
= 
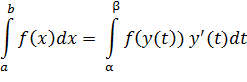

 α =0
α =0 =
=  = 2
= 2  = 2(
= 2( ) = 2(t
) = 2(t  - arctg t
- arctg t  = 2(-0-arctg2+arctg0) = 2(2-arctg2)/
= 2(-0-arctg2+arctg0) = 2(2-arctg2)/ =
=  - t
- t  =
= (0-1) =
(0-1) =  ;
;
 UV
UV  Поэтому имеем
Поэтому имеем =
= 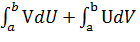 откуда следует
откуда следует 
 Формула интегрирования по частям
Формула интегрирования по частям =
=  -
-  =
= 
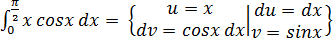 = x sin x
= x sin x 
 x sin x
x sin x  cos x
cos x  =
= 



