Если тело образовано вращением вокруг оси Ox криволинейной трапеции,
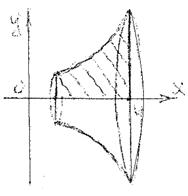 Рис 8.1 Рис 8.1
| которая ограничена кривой y=f(x), прямыми линиями x=a, x=b (a< b) и осью Ox (рис.8.1), то его объем определяется по формуле:
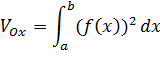
|
Если тело образовано вращением вокруг оси Oy криволинейной трапеции
которая ограничена кривой x =φ (y), прямыми линиями y=c, y=d (c< d) и осью Оy (рис 8.2) то его объем определяется по формуле:
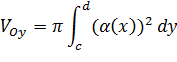
| Рис 8.2 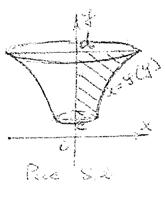
|
Пример 1. Найти объем тела, образованного вращением вокруг оси Ox фигуры, ограниченной линиями y=4x-x2 и y=0.

| Решение:
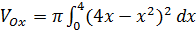 = = 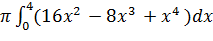 = = 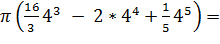 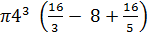 =
512/12π (ед3) =
512/12π (ед3)
|
Пример 2. Найти объем тела, образованного вращением вокруг оси Oy фигуры, ограниченной линиями xy=2; y=1; y=3; x=0

| Решение:
x y=2 ⟹ x=2/y – гипербола
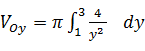 = 4π = 4π 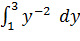 = 4π (-1/y) = 4π (-1/y)   (ед3) (ед3)
|
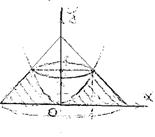
Пример 3 Найти объем тел, образованных вращением фигуры, ограниченной линиями y=x2; x+y=2; y=0 (в четверти) 1) вокруг оси Ox 2) вокруг оси Oy

| Решение
Объем тела, образованного вращением фигуры вокруг оси Ox найдем как сумму объемов двух тел, одно из которых образовано вращением фигуры y=x2, x=1, y=0, а второе y=2-x, x=1 y=0 (в 1й четверти) 1) вокруг оси Ох 2) вокруг оси Oy
|
 +
+ 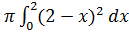 =
= 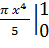 + π (4x-
+ π (4x- 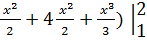 =
=
= π 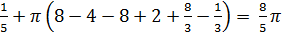 ед3
ед3
|
Объем тела, образованного вращением той же фигуры вокруг оси Oy найдем как разность объемов двух тел, из которых большее образовано вращением фигуры x+y=2; x=0, y=0, y=1, а меньшее y=x2, x=0, y=1.
|
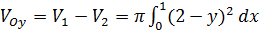 -
- 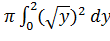 =
= 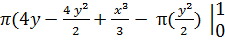 =
=
= π 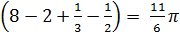 ед3
ед3

 Рис 8.1
Рис 8.1
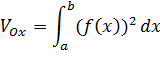
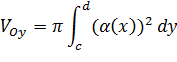


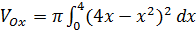 =
= 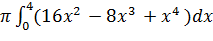 =
= 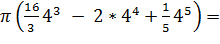
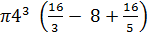 =
512/12π (ед3)
=
512/12π (ед3)

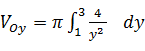 = 4π
= 4π 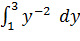 = 4π (-1/y)
= 4π (-1/y) 
 (ед3)
(ед3)

 +
+ 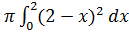 =
= 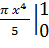 + π (4x-
+ π (4x- 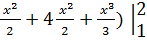 =
=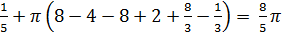 ед3
ед3
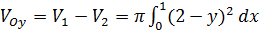 -
- 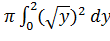 =
= 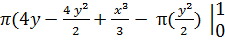 =
=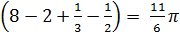 ед3
ед3


