
| 1) Если на отрезке[a, b] функция f(x)  , то площадь криволинейной трапеции, ограниченной кривой y= f(x), осью Ox и прямыми x=a и x=b (рис.1) равна: , то площадь криволинейной трапеции, ограниченной кривой y= f(x), осью Ox и прямыми x=a и x=b (рис.1) равна:

|

| 2) Если f(x)  на отрезке [a, b], то на отрезке [a, b], то  , тогда площадь соответствующей криволинейной трапеции , тогда площадь соответствующей криволинейной трапеции
 Если f2(x)
Если f2(x)  f1(x) при x f1(x) при x  [a, b] то площадь фигуры (рис.2), ограниченной кривыми y=f1(x); y=f2(x) и прямыми x=a и x=b находятся по формуле [a, b] то площадь фигуры (рис.2), ограниченной кривыми y=f1(x); y=f2(x) и прямыми x=a и x=b находятся по формуле

|

| 3) Если криволинейная трапеция прилежит к оси OY (рис.3) и ограничена линиями x= α (y) осью OY y=c и y=d, то площадь криволинейной трапеции 
|
4) Если кривая задана параметрическими уравнениями x=x(t), y=y(t)≥ 0, то площадь криволинейной трапеции, ограниченной этой кривой, прямыми x=a, x=b и отрезком [a, b] оси Ox, выражается формулой: 
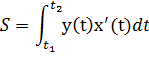
где  и
и  определяются из уравнений a=x(t1), b=x(t2).
определяются из уравнений a=x(t1), b=x(t2).

| 5) Площадь криволинейного сектора (рис 4), ограниченного кривой, заданной в полярных координатах лучами ρ = ρ (y) и двумя полярными лучами y=α и y=β (α < β), выражается интегралом

|
Пример1. Вычислить площадь фигуры, ограниченной линиями y=x2–3x и y=x.
Решение

|
Решая совместно уравнения, находим точки пересечения параболы и прямой:
   ⟹ x(x-4)=0⟹ x1=0; x2=4
Поскольку на [0, 4] y2(x)≥ y1(x) то площадь фигуры найдем по формуле:
⟹ x(x-4)=0⟹ x1=0; x2=4
Поскольку на [0, 4] y2(x)≥ y1(x) то площадь фигуры найдем по формуле:
 
 = 4 = 4 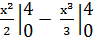 = 2*16-64/3= 32-64/3 = 32/3 (ед2) = 2*16-64/3= 32-64/3 = 32/3 (ед2)
|
Пример 2. Найти площадь фигуры, ограниченной первой аркой циклоиды
x=2(t-sin t), y=2(1-cos t) 0≤ t≤ 2π и осью Ox.
Решение

| 
 = =  = 4(t-2sin t +1/2t + ¼ sin2t) = 4(t-2sin t +1/2t + ¼ sin2t)  =
=12π (ед2) =
=12π (ед2)
|
Пример 3. Найти площадь фигуры, ограниченной кардиоидой ρ =α (1+cos y)
Решение

| В силу симметрии фигуры S=2S1= 2*1/2
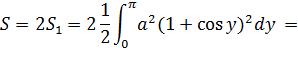 =
=  = =  = =  (ед2) (ед2)
|


 , то площадь криволинейной трапеции, ограниченной кривой y= f(x), осью Ox и прямыми x=a и x=b (рис.1) равна:
, то площадь криволинейной трапеции, ограниченной кривой y= f(x), осью Ox и прямыми x=a и x=b (рис.1) равна:


 на отрезке [a, b], то
на отрезке [a, b], то  , тогда площадь соответствующей криволинейной трапеции
, тогда площадь соответствующей криволинейной трапеции
 Если f2(x)
Если f2(x)  f1(x) при x
f1(x) при x  [a, b] то площадь фигуры (рис.2), ограниченной кривыми y=f1(x); y=f2(x) и прямыми x=a и x=b находятся по формуле
[a, b] то площадь фигуры (рис.2), ограниченной кривыми y=f1(x); y=f2(x) и прямыми x=a и x=b находятся по формуле




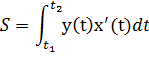
 и
и  определяются из уравнений a=x(t1), b=x(t2).
определяются из уравнений a=x(t1), b=x(t2).




 ⟹ x(x-4)=0⟹ x1=0; x2=4
Поскольку на [0, 4] y2(x)≥ y1(x) то площадь фигуры найдем по формуле:
⟹ x(x-4)=0⟹ x1=0; x2=4
Поскольку на [0, 4] y2(x)≥ y1(x) то площадь фигуры найдем по формуле:


 = 4
= 4 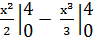 = 2*16-64/3= 32-64/3 = 32/3 (ед2)
= 2*16-64/3= 32-64/3 = 32/3 (ед2)


 =
=  = 4(t-2sin t +1/2t + ¼ sin2t)
= 4(t-2sin t +1/2t + ¼ sin2t)  =
=12π (ед2)
=
=12π (ед2)

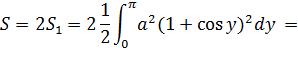 =
=  =
=  =
=  (ед2)
(ед2)



