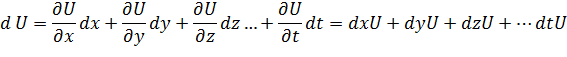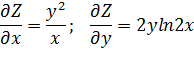Частные производные функции нескольких переменных
Определение: Частной переменной по x от функции Z=f(x, y) называется предел отношения частного приращения по x: к приращению Z’x; f’x(x, y) Аналогично частной производной по y от функции Z=f(x, y) называется предел отношения частного приращения по y
к приращению по y стремлении Z’y; f’y(x, y) Частные производные можно определить так: частной производной по x от функции Z=f(x, y) называется производная по x, выраженная в предположении что y – постоянная. Частной производной по y от функции Z=f(x, y) называется производная по y, вычисленная в предположении что x- постоянная. Поэтому правила вычисления частных производных совпадают с правилами дифференцирования, функций одной переменной, только надо каждый раз помнить, по какой переменной ищется производная. Пример 1 Z= arc sin x/y
Пример 2.
Аналогично определяются частные производные функций любого числа переменных. Пример 3. U=2x3-3y2+sinz2
9.3. Дифференциальная функция нескольких переменных. Полное приращение функции Z=f(x, y) равно:
Оно может быть представлено в виде:
Где
Определение: Полным дифференциалом функции двух переменных называется главная часть полного приращения функции, линейная относительно приращений независимых переменных по
Обозначается dZ или df так что dz=f’x (x, y) Δ x+ f’y (x, y) Δ y Тогда Δ Z= dz+ Δ Z≈ dz Приращения Δ x и Δ у независимых переменных называются дифференциалами независимых переменных и обозначаются Δ x= dx; Δ у= dy; тогда
Т.е. полный дифференциал равен сумме произведений частных производных на дифференциалы соответствующих независимых переменных. Определение: Частным дифференциалом по x функции Z=f(x, y) называется главная часть частного приращения Δ xZ=f(x+ Δ x, y)- f(x, y), пропорциональная приращению x независимой переменной x.
Аналогично
Частный дифференциал функции двух независимых переменных равен произведению соответствующей частной производной на дифференциал этой производной. На основании рассмотренного выше заключаем, что полный дифференциал функции равен сумме ее частных дифференциалов. Если U=f(x, y, z….t), то частичные и полный дифференциалы определяются соответственно аналогично:
Пример: Найти полный дифференциал функции Z=y2 ln 2x 1) Находим частные производные функций;
2) Составляем частные дифференциалы;
3) Полный дифференциал найдем как суму частных дифференциалов
|


 при стремлении
при стремлении 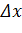 к нулю обозначается
к нулю обозначается так что
так что 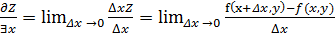

 к нулю; обозначается
к нулю; обозначается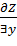 так что
так что 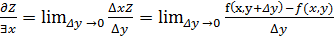

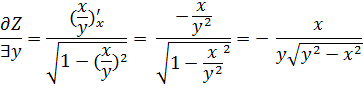



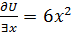
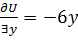



 и
и  – бесконечно малые величины по
– бесконечно малые величины по 
 +
+  и с точностью до бесконечно малых высшего порядка
и с точностью до бесконечно малых высшего порядка
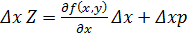 , следовательно,
, следовательно,