Матрицы и определители
Матрицей называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Матрица записывается в виде:
или сокращенно как А=(aij), где i= 1, 2, …, m; i =1, 2, …, n. Матрица, содержащая один столбец или одну строку, называется вектором или вектором-столбцом, вектором-строкой соответственно. Матрица, у которой число строк равно числу столбцов и равно n, называется квадратной матрицей n-го порядка. Диагональной называется квадратная матрица, у которой все элементы вне главной диагонали (т.е. с индексами i¹ j) равны нулю. Единичной называется диагональная матрица с единицами на главной диагонали (обозначается Е). Нулевой называется матрица, все элементы которой равны нулю. Примеры матриц: а) квадратная; б) диагональная; в) единичная; г) нулевая: а) Каждой квадратной матрицей n -го порядка можно поставить в соответствие число Δ (detA), называемое ее определителем. При n=1 А=(а 1); Δ =detA= а 1. При n=2 При n=3 Δ = -a32a23a11. Для вычисления определителей второго и третьего порядков можно пользоваться следующими схемами:
Основные свойства определителей: 1. Значение определителя не изменяется, если заменить его строки столбцами и наоборот. 2. При перестановке двух параллельных рядов определитель меняет знак. 3. Определитель, имеющий два одинаковых ряда, равен нулю. 4. Общий множитель элементов какого-либо ряда можно вынести за знак определителя в качестве сомножителя. 5. Определитель не изменится, если к элементам одного ряда прибавить элементы параллельного ряда, умноженные на одно и то же число.
Минором некоторого элемента aij определителя n-го порядка называется определитель (n-1)-го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых стоит элемент аij. Обозначается минор как Мij. Алгебраическим дополнением элемента aij называется минор Мij, умноженный на (-1) i+j, т.е. Аij =(-1) i+jMij. Определитель любого порядка можно представить как сумму произведений элементов какого-либо ряда определителя на соответствующие им алгебраические дополнения.
_________________
1.1.1. Вычислить определители: а) Ответ: а) 26; б) 7; в) 1. 1.1.2. При каких значениях а обращается в ноль определитель Δ = Ответ: ±2 1.1.3. Вычислить определитель по правилу треугольников а) Ответ: а) 47; б)0. 1.1.4. При каких значениях а обращается в ноль определитель
Ответ: (1; -2) 1.1.5. Вычислить определитель путем разложения по элементам 3-го столбца
Ответ: (-48). 1.1.6. Вычислить определитель с помощью разложения по элементам второй строки
Ответ: (-15). 1.1.7. Вычислить определители а) Ответ: а) 0, б) 28. 1.1.8. Вычислить определители
Ответ: а) -38; б) 27; в) -1; г) 2 а; д) sin 2a- sin 2b. 1.1.9. Вычислить определитель с помощью разложения по элементам какого-либо ряда и проверить по правилу треугольников
Ответ: а) 73; б) 23. 1.1.10. Упростить и вычислить определители:
Ответ: а) -156; б) 0. 1.1.11. Решить уравнение
Ответ: (2; 3).
|

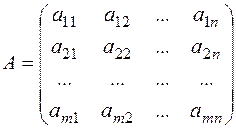
 ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.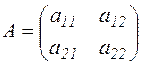 ; Δ = a11a22-a12a22.
; Δ = a11a22-a12a22. ;
; = a11a22a33+a12a23a31+a21a32a13-a13a22a31-a21a12a33-
= a11a22a33+a12a23a31+a21a32a13-a13a22a31-a21a12a33- при n=2;
при n=2;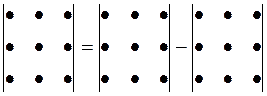 при n=3.
при n=3. ; б)
; б)  ; в)
; в)  .
. ?
? .
. ?
?
 .
. .
.
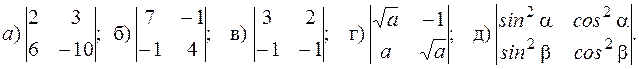


 .
.


