Векторы. Линейные операции над векторами
Геометрическийвектор Длиной вектора (модулем) называют длину отрезка [АВ]. Векторы обозначают как Два вектора называются равными, если они имеют равные длины и одинаковое направление. Вектор, начало и конец которого совпадают, называется нулевым Произведением вектора Суммой нескольких векторов называется вектор, проведенный из начала первого вектора в конец последнего при условии, что начало каждого последующего вектора совмещается с концом предыдущего. Проекцией вектора Если векторы Пусть имеется трехмерная прямоугольная система координат, в которой задана точка М(x, y, z). Радиусом – вектором точки М называется вектор Длина радиуса – вектора определяется как Единичные векторы координат осей
Углы α, β, γ между вектором ______________
2.1.1. По сторонам ОА и ОВ прямоугольника ОАСВ отложены единичные векторы Ответ:
2.1.2. Проверить аналитически и геометрически векторные тождества а) Ответ: 2.1.3. В треугольной пирамиде SABC, где S – вершина, даны векторы Ответ: 2.1.4. Даны векторы Ответ: 2.1.5. В параллелограмм АВСД заданы вершина С(6; -8; 5) и векторы АС={-3; 1; 4}, ВД={2; -3; 5} – его диагонали. Определить координаты точки В. Ответ: В(6, 5; -7; 0, 5). 2.1.6. Построить вектор Ответ: | 2.1.7. В прямоугольной системе координат даны векторы Ответ: 2.1.8. Построить параллелограмм на векторах Ответ: ____________
2.1.9. На плоскости даны точки А(3; 3); В(-3; 3); С(-3; 0); О(0; 0). Построить вектор Ответ: 2.1.10. Определить координаты центра тяжести треугольника АВС, если А(5; 1; 12); В(11; 3; 8); С(2; 5; 0). 2.1.11. Построить точку М(5; -3; 4). Определить длину и направление ее радиус – вектора. Ответ: 2.1.12. Вектор 2.1.13. Даны векторы Ответ: 2.1.14. Даны три последовательные вершины параллелограмма А(1; -2; 3); В(3; 2; 1); С(6; 4; 4). Найти координаты его четвертой вершины. Ответ: Д(4; 0; 6).
|

 - это направленный отрезок, у которого один конец (точка А) называется началом вектора, а другой конец (точка В) – концом вектора.
- это направленный отрезок, у которого один конец (точка А) называется началом вектора, а другой конец (точка В) – концом вектора. , а их длины
, а их длины  .
. .
. на некоторое число α Î R называется вектор, длина которого равна длине вектора
на некоторое число α Î R называется вектор, длина которого равна длине вектора  заданы своими координатами, т.е
заданы своими координатами, т.е  , то вектор k
, то вектор k  1, k
1, k 
 ,
, 
 , …,
, …, 
 .
. , соединяющий начало координат с этой точкой.
, соединяющий начало координат с этой точкой. ;
; называются ортами. Радиус – вектор через орты выражается как
называются ортами. Радиус – вектор через орты выражается как  . Если вектор
. Если вектор  ;
; .
. , причем cos2α +cos2β +cos2γ =1.
, причем cos2α +cos2β +cos2γ =1. . М – середина стороны ВС, N – середина АС. ОА =3, ОВ=4. Выразить через
. М – середина стороны ВС, N – середина АС. ОА =3, ОВ=4. Выразить через  векторы
векторы 
 .
.

 ; б)
; б)  .
. . Найти вектор
. Найти вектор 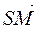 , где М – центр тяжести основания АВС.
, где М – центр тяжести основания АВС. .
. . Вектор
. Вектор  - медиана Δ ОАВ. Разложить аналитически и геометрически вектор
- медиана Δ ОАВ. Разложить аналитически и геометрически вектор 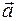 по векторам
по векторам  .
.
 . Определить его длину и направление.
. Определить его длину и направление. и
и  . Найти длину и направление вектора
. Найти длину и направление вектора  .
. .
. =
= 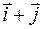 и
и  =
= 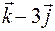 . Определить его диагонали.
. Определить его диагонали. =
=  ;
;  .
. . Выразить векторы
. Выразить векторы  через единичные векторы
через единичные векторы 
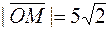 .
. .
.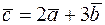 .
. .
.


