Уравнением линии на плоскости ХОУ называется такое уравнение F(x, y)=0 с двумя переменными, которому удовлетворяют координаты х и у каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на линии.
Переменные х и у в уравнении линии называются текущими координатами точек линии.
Простейшей из линий является прямая.
Разным способам задания прямой соответствуют в прямоугольной системе координат различные виды ее уравнений (табл. 1).
Таблица 1
| №
п/п
| Вид уравнения
| Смысл входящих в уравнение коэффициентов
| Примечания
|
|
| Уравнение с угловым коэффициентом y=kx+b
| k – тангенс угла a наклона прямой к положительному направлению оси ОХ; b – отрезок, отсекаемый прямой от оси ОY
| a≠ π /2
|
|
| Общее уравнение прямой Ах+Ву+С=0
| А, В – координаты вектора, перпендикулярного прямой (нормального вектора) N.
| А, В не равны нулю одновременно
|
|
| Уравнение прямой, про-ходящей через данную точку в данном направ-лении у-у0=k(х-х0)
| т.М(х0, у0) – заданная точка; k – угловой коэффициент прямой
| При различных k уравнение называется уравнением пучка прямых с центром в точке М(х0, у0)
|
|
| Уравнение прямой, проходящей через две заданные точки 
| т.М1(х 1, у 1), т.М2(х 2, у 2) – заданные точки
|
|
|
| Уравнение прямой в отрезках на осях х  . .
| а, b – отрезки, отсекаемые прямой от координатных осей ОХ и ОY соответственно
| а ≠ 0, b ≠ 0
|
|
| Уравнение прямой, проходящей через заданную точку параллельно заданному вектору 
| т.М0(х 0, у 0) – заданная точка; m, n – координаты вектора, параллельного искомой прямой (направляющего век-тора) 
| Такое уравнение часто называют каноническим
|
| №
п/п
| Вид уравнения
| Смысл входящих в уравнение коэффициентов
| Примечания
|
|
| Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору А(х-х 0)+В(у-у 0)=0
| т.М0(х 0, у 0) – заданная точка, А, В – координаты нормального вектора искомой прямой 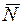
|
|


 .
.