Свойства векторного произведения
1. 2. 3. Векторное произведение ортов
движение осуществляется слева направо, то знак векторного произведения положи- тельный, в противном случае – отрицательный, т.е. Если заданы два вектора
Применение векторного произведения
1. Площадь треугольника, построенного на векторах 2. Условие коллинеарности двух векторов 3. Момент силы
________________
2.3.1. Построить векторы 2) Ответ: 2.3.2. Раскрыть скобки и упростить выражения: 1) 2) Ответ: 1) 2.3.3. Даны векторы Ответ: 2.3.4. Даны векторы Ответ: 2.3.5. Найти площадь треугольника с вершинами А(1; 2; 0); В(3; 0; -3); С(5; 2; 6). Ответ: 14. 2.3.6. Найти площадь параллелограмма, построенного на векторах Ответ: 2.3.7. Найти площадь параллелограмма, диагоналями которого служат векторы Ответ: 2.3.8. Сила Ответ: 2.3.9. Построить векторы Ответ: 2.3.10. Раскрыть скобки и упростить выражения: 1) 2) Ответ: 1) 2.3.11. Даны векторы Ответ: 2.3.12. Дан треугольник с вершинами А(2; -1; 2); В(1; 2; -1); С(3; 2; 1). Найти его площадь. Ответ: 2.3.13. Найти площадь параллелограмма, построенного на векторах Ответ: 1, 5.
|

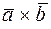 = -
= -  .
.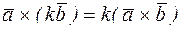 .
. .
. .
. Для перемножения ортов между собой можно воспользоваться следующей схемой (рис.1). Векторное произведение двух последовательно стоящих ортов равно следующему за ними орту, при этом если
Для перемножения ортов между собой можно воспользоваться следующей схемой (рис.1). Векторное произведение двух последовательно стоящих ортов равно следующему за ними орту, при этом если ,
,  и тд.
и тд. своими координатами в ортонормированном базисе как
своими координатами в ортонормированном базисе как  , то
, то  .
. .
. .
. , приложенный в точке А, равен
, приложенный в точке А, равен  .
. , если 1)
, если 1)  ;
; и
и  .
.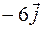 ; 0.
; 0. ;
; .
. ; 2)
; 2)  .
. =
=  ,
,  =
=  . Найти
. Найти 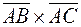 .
. .
. Найти
Найти  .
. .
. - единичные векторы, угол между которыми равен π /3.
- единичные векторы, угол между которыми равен π /3. .
. - единичные векторы, образующие угол 45°.
- единичные векторы, образующие угол 45°. приложена в точке М(2; -1; 1). Найти ее момент относительно начала координат.
приложена в точке М(2; -1; 1). Найти ее момент относительно начала координат. .
.
 ; 2)
; 2) 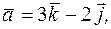
 .
. .
. ;
; .
. ; 2) 3.
; 2) 3.
 . Найти векторное произведение
. Найти векторное произведение  .
. .
. .
. - единичные векторы с углом между ними 30°.
- единичные векторы с углом между ними 30°.


