Операции над матрицами
Суммой матриц А = (aij) и В = (bij) одинакового размера называется матрица С = (сij) того же размера, причем сij = aij + bij, " i, j. Свойства операции сложения матриц
Для любых матриц А, В и С одного размера выполняются равенства: 1. А+В=В+А (коммутативность); 2. (А+В)+С=А+(В+С)=А+В+С (ассоциативность). Произведением матрицы А = (aij) на число l называется матрица В = (bij) того же размера, что и матрица А, причем bij =l aij, " i, j. Свойства операции умножения матрицы на число
1. l(mА)=(l m) А (ассоциативность). 2. l(А+В)= l А +l В (дистрибутивность относительно сложения матриц). 3. (l+ m) А =l А+mА (дистрибутивность относительно сложения чисел). Произведением АВ матриц А и В (размеров m ´ n и n ´ r соответственно) называется матрица С размера m ´ r, такая, что сij = ai 1 b 1 j+ a 12 b 2 j +…+ aik bkj +…+ ain bnj = Таким образом, каждый элемент сij, находящийся в i -й строке и j -м столбце матрицы С, равен сумме произведений соответствующих элементов i -й строки матрицы А и j -го столбца матрицы В. Получение элемента сij схематично изображается так
j Произведение АВ существует, только если число столбцов матрицы А равно числу строк матрицы В.
Свойства операции умножения матриц
1. (АВ)С=А(ВС)=АВС (ассоциативность). 2. (А+В)С=АС+ВС (дистрибутивность). 3. А(В+С)=АВ+АС (дистрибутивность). 4. АВ¹ ВА (отсутствует коммутативность). Коммутирующими (или перестановочными) называются матрицы А и В, для которых АВ=ВА. Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной к данной (обозначается А Т). _________________
1.3.1. Найти линейные комбинации заданных матриц: а) А- l Е, б) 4 А -5 В, 1.3.2. Найти произведения матриц АВ и ВА (если они существуют): а) в) 1.3.3. Проверить, коммутируют ли матрицы: а) б) 1.3.4. Найти произведения матриц АА Т и А Т А: а) 1.3.5. Найти линейные комбинации матриц: а) 5 А -3 В +2 С, б) А- l Е, 1.3.6. Найти произведения АВ и ВА (если это возможно): а) 1.3.7. Найти произведения АА Т и А Т А: а) ________________________ Ответы: 1.3.1. а) 1.3.2. а) б) АВ =(31); в) АВ не существует, 1.3.3. а) да; б) нет. 1.3.4. а) б) АА Т=(30); в) 1.3.5. а) 1.3.6. а) б) 1.3.7. а) б)
|

 .
.





 ;
; .
. ; б) А =(4 0 -2 3 1),
; б) А =(4 0 -2 3 1),  ;
; .
. ;
; .
. б) А =(1 2 3 4); в)
б) А =(1 2 3 4); в)  .
. ;
; .
. ; б)
; б)  .
.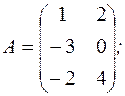 б)
б)  .
. ; б)
; б)  .
. ;
; ;
; .
. ;
; ;
; ;
;  .
. б)
б)  .
. , ВА – не существует;
, ВА – не существует; ;
;  .
. ;
; .
.


