С m неизвестными
Система m линейных уравнений с m неизвестными имеет вид:
Определитель, составленный из коэффициентов при неизвестных
называется главным определителем системы. Если Δ ≠ 0, то система имеет единственное решение, которое может быть найдено по правилу Крамера:
Определители Δ xi получаются из главного определителя системы путем замещения элементов i-го столбца столбцом свободных членов. Пример. Решить систему уравнений
Другим способом решения систем линейных уравнений является метод Гаусса или метод исключения, который состоит из двух этапов. На первом этапе путем линейных преобразований уравнений системы заданная система приводится к ступенчатому, в частности, треугольному виду; на втором этапе определяются значения неизвестных. В качестве примера решим систему (1) методом Гаусса. Разделим все члены первого уравнения системы (1) на коэффициент а 11=2. Получим систему
Умножим все члены первого уравнения на 3 и вычтем их из второго уравнения, затем из третьего уравнения вычтем первое, само первое уравнение системы (2) оставим без изменения. Тогда будем иметь
Разделим все члены второго уравнения на 0, 5:
Умножим второе уравнение на -0, 5 и вычтем его из третьего, при этом первое и второе уравнения системы (4) оставим без изменения
На этом завершен так называемый прямой ход метода Гаусса. Неизвестные находятся в обратной последовательности. Из последнего уравнения находим х 3=3, из второго следует х 2, из первого х 1=0, 5-0, 5∙ 2+0, 5∙ 3=1. Замечания. Следует иметь в виду, что если главный определитель системы Δ ≠ 0, то система имеет единственное решение. Если Δ =0, но хотя бы один из определителей Δ х i ≠ 0, то система не имеет решений. Если Δ =0 и все определители Δ х i =0, то система имеет бесчисленное множество решений. ______________
1.2.1. Решить системы уравнений по правилу Крамера: а) Ответ: а) (0; 2); б) (5; 6; 10); в) (-1; 0; 1).
1.2.2. Решить систему уравнений двумя способами: по правилу Крамера и методом Гаусса.
Ответ: (2; -1; -3).
1.2.3. Решить системы уравнений методом Гаусса а) в) Ответ: а) решений нет; б) решений бесконечное множество; в) (1; -1; 2; 3). ____________
1.2.4. Решить системы уравнений по правилу Крамера а) Ответ: а) (5; -4); б) (2; -5; 3).
1.2.5. Решить систему уравнений двумя способами
Ответ: (2; 1; 3).
1.2.6. Решить систему методом Гаусса
Ответ: (3; -4; -1; 1).
|

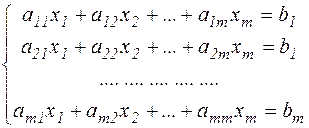 .
.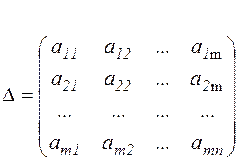 ,
,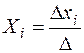 , где i=1, 2, …, m.
, где i=1, 2, …, m.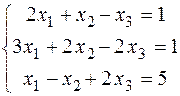 . (1)
. (1)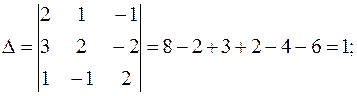
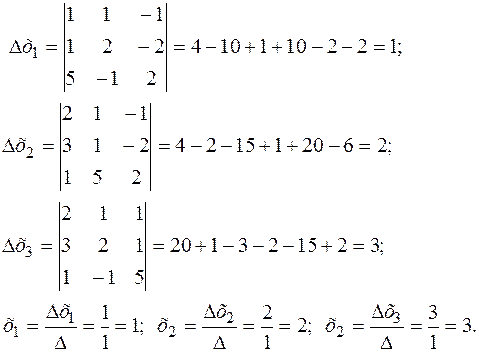
 . (2)
. (2)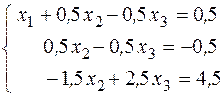 . (3)
. (3)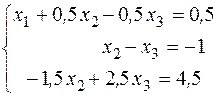 . (4)
. (4)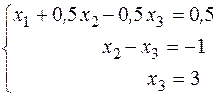 . (5)
. (5)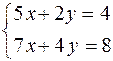 ; б)
; б)  ; в)
; в)  .
.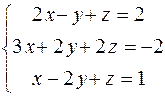 .
.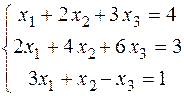 ; б)
; б) 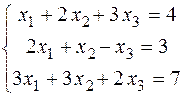 ;
;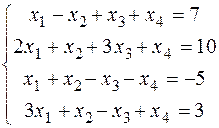 .
.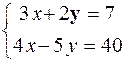 ; б)
; б)  .
. .
.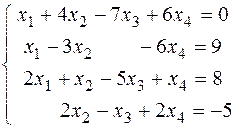 .
.


