Матричные уравнения и системы линейных уравнений
Обратной матрицей к квадратной матрице А называется такая матрица (обозначается А -1), что А -1 А=А А -1= Е. Замечание. Если матрица А -1 существует, то она единственна. Минором Мij к элементу аij квадратной матрицы А называется определитель, вычисленный из элементов матрицы А, оставшихся после вычеркивания i -й строки и j -го столбца. Алгебраическим дополнением Аij к элементу аij квадратной матрицы А=(aij) называется произведение Аij= (-1) i+jMij. Присоединенной матрицей к квадратной матрице А=(aij) называется матрица Теорема. Если квадратная матрица А – невырожденная (т.е. det A ¹ 0), то
Метод присоединенной матрицы вычисления обратной матрицы к невырожденной матрице А состоит в применении формулы (*). Матричные уравнения простейшего вида с неизвестной матрицей Х записываются следующим образом: АХ=В, ХА=В, АХС=В. В этих уравнениях А, В, С, Х – матрицы таких размеров, что все используемые операции умножения возможны, и с обеих сторон от знака равенства стоят матрицы одинаковых размеров. Если в этих уравнениях матрицы А и С невырожденные, то их решения записываются следующим образом: а) для уравнения АХ=В Þ Х=А -1 В; б) для уравнения ХА=В Þ Х=ВА -1; в) для уравнения АХС=В Þ Х=А -1 ВС -1.
|
, составленная из алгебраических дополнений Аij к элементам aij матрицы А.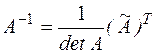
. (*)
