Смешанное произведение трех векторов
Смешанным произведением трех векторов Свойства смешанного произведения 1. 2. 3. 4. Если три вектора заданы своими координатами в ортонормированном базисе как
Применение смешанного произведения 1. Объем параллелепипеда, построенного на векторах 2. Объем пирамиды, построенной на векторах 3. Условие компланарности трех векторов ___________
2.4.1. Найти объем пирамиды, вершинами которой служат точки А(1; 2; 3); В(0; -1; 1); С(2; 5; 2); Д(3; 0; -2). Ответ: 4. 2.4.2. Найти объем параллелепипеда, построенного на векторах Ответ: 24. 2.4.3. Доказать, что векторы 2.4.4. Доказать, что точки А(2; -1; -2); В(1; 2; 1); С(2; 3; 0); Д(5; 0; 6) лежат в одной плоскости. Ответ: не лежат. _______________
2.4.5. Задана пирамида с координатами своих вершин: А(2; 0; 0); В(0; 3; 0); С(0; 0; 6) и Д(2; 3; 8). Вычислить ее объем и высоту, опущенную на грань АВС. Ответ: 14; 2.4.6. Найти объем параллелепипеда, построенного на векторах Ответ: 51. 2.4.7. Проверить компланарность векторов Ответ: компланарны.
|
называется произведение, которое получается скалярным умножением векторного произведения двух векторов на третий вектор, то есть произведение вида 
или иначе 
.
= 
.
.
.
.
, то
.
| 
.
компланарны.
.
.
.
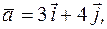
