Кривые второго порядка на плоскости
Уравнение вида А х 2+2В ху +С у 2+2D х +2Е у +F=0 называется общим уравнением кривой второго порядка. Коэффициенты уравнения – действительные числа, причем хотя бы одно из чисел А, В, С отлично от нуля. Такое уравнение определяет на плоскости окружность, эллипс, гиперболу или параболу. В табл. 3 приведены уравнения кривых второго порядка и определен смысл входящих в них коэффициентов.
Таблица 3
______________
3.2.1. Найти координаты фокусов и эксцентриситет эллипса Ответ: ±3; 0; 0, 6. 3.2.2. Составить каноническое уравнение эллипса, у которого а) большая полуось равна 10, эксцентриситет равен 0, 8; б) малая полуось равна Ответ: 3.2.3. Эллипс, симметричный относительно осей координат, проходит через точки М(2; Ответ: 3.2.4. Построить гиперболу х 2-4 у 2=16 и ее асимптоты. Найти фокусы, эксцентриситет, угол между асимптотами. Ответ: 3.2.5. Написать каноническое уравнение гиперболы, зная, что: а) расстояние между фокусами равно 10, между вершинами равно 8; б) вещественная полуось равна Ответ: 3.2.6. Написать уравнение гиперболы, имеющей вершины в фокусах, а фокусы – в вершинах эллипса Ответ: 3.2.7. Написать уравнения прямых, проходящих через левую вершину гиперболы Ответ: а)3 х -2 у +6Ö 5=0, б) 3.2.8. Парабола с вершиной в начале координат проходит через точку А(2; 4) и симметрична относительно оси ОХ. Написать ее уравнение. Ответ: у 2=8 х. 3.2.9. Написать каноническое уравнение эллипса, зная, что его большая полуось а =12, эксцентриситет равен 0, 5. Найти расстояние между фокусами. Ответ: 3.2.10. Определить полуоси, координаты фокусов, эксцентриситет эллипса 3 х 2+4 у 2-12=0. Ответ: а =2; b =Ö 3; с =1; e =0, 5. 3.2.11. Написать уравнение прямой, проходящей через нижний правый фокус эллипса Ответ: у = х -3. 3.2.12. Определить фокусы, вершины, эксцентриситет и асимптоты гиперболы Ответ: F1(0; -5); F2(0; 5), 3.2.13. Написать каноническое уравнение гиперболы, проходящей через точки А(2; 1), В(-4; Ö 7). Ответ: 3.2.14. Написать уравнение прямой, проходящей через левую вершину гиперболы Ответ: 3.2.15. Парабола с вершиной в начале координат проходит через точку А(1; -2) и симметрична относительно оси ОY. Написать уравнение параболы, найти координаты фокуса и уравнение директрисы. Ответ: у = -2 х 2; F(0; -1/8); у =1/8.
|

 Эллипс – множество всех точек плоскости, сумма расстояний от которых до двух точек, называемых фокусами, есть величина постоянная (рис.2)
Эллипс – множество всех точек плоскости, сумма расстояний от которых до двух точек, называемых фокусами, есть величина постоянная (рис.2)
 - каноническое уравнение эллипса
- каноническое уравнение эллипса
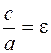 - эксцентриси-тет, 0< e < 1.
Т. А1, А2, В1, В2 – вершины эллипса
- эксцентриси-тет, 0< e < 1.
Т. А1, А2, В1, В2 – вершины эллипса

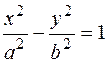 - каноническое уравнение гиперболы
- каноническое уравнение гиперболы
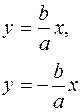 - асимптоты
- асимптоты
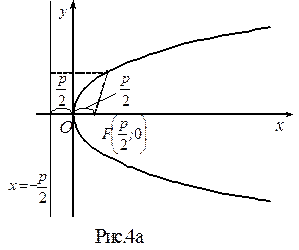

 - фокус,
- фокус,
 ди-ректриса.
Точка (0; 0) – вершина параболы (рис.3а)
F
ди-ректриса.
Точка (0; 0) – вершина параболы (рис.3а)
F 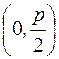 - фокус,
- фокус,
 ди-ректриса.
Точка (0; 0) – вершина параболы (рис.4б)
ди-ректриса.
Точка (0; 0) – вершина параболы (рис.4б)
 . Построить эллипс.
. Построить эллипс. , расстояние между фокусами равно 8.
, расстояние между фокусами равно 8. ;
;  .
. ) и В(0; 2). Написать его уравнение. Построить кривую.
) и В(0; 2). Написать его уравнение. Построить кривую. .
. .
. , эксцентриситет равен
, эксцентриситет равен  .
.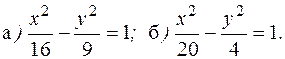
 .
. .
. 1 а) параллельно прямой 3 х -2 у +6=0; б) перпендикулярно асимптоте, образующей острый угол с осью ОХ.
1 а) параллельно прямой 3 х -2 у +6=0; б) перпендикулярно асимптоте, образующей острый угол с осью ОХ. .
. ; 2 с =12.
; 2 с =12.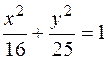 под углом 45° к оси ОХ.
под углом 45° к оси ОХ. . Сделать эскиз.
. Сделать эскиз. .
. .
. и отсекающую от оси ОY отрезок 5 единиц.
и отсекающую от оси ОY отрезок 5 единиц. .
.


