Некоторые свойства и графики
Переменная величина у называется функцией переменной величины х, если каждому значению х ставится в соответствие одно определенное значение у. Х – множество значений переменной х, которое называется областью определения функции и обозначается D(f). Y – множество значений переменной величины у, обозначаемое как E(f). Основными элементарными функциями являются следующие аналитически заданные функции: 1. Степенная функция у=х a, aÎ R. 2. Показательная функция у=ах, а > 0, а ≠ 1. 3. Логарифмическая функция y=logax, a > 0, а ≠ 1. 4. Тригонометрические функции y=sinx, y=cosx, y=tgx, y=ctgx. 5. Обратные тригонометрические функции y=arcsinx, y=arccosx, y=arctgx, y=arcctgx. Элементарная функция может быть сложной, то есть являться функцией от некоторой функции, например y=f(u), u=j(х), тогда y=f(j(x)). Различают четные и нечетные функции, периодические и непериодические, функции общего вида. ________________
4.1.1. Задана функция Найти Ответ: 4.1.2. Найти область определения функций D(f): а) г) Ответ: (-µ; -1)È (-1; +µ); (-µ; -2)È (-2; 2)È (2; +µ); (-3; 3); (-µ; -2)È (2; +µ); (-µ; 2]È [5; +µ); [-6; 2]. 4.1.3. Найти множество значений функции E(f): а) f(x)=x 2+4 x +3; б) f(x)= 2| x |; в) f(x) =3-5 cosx; г) f(x)= | x |-3; д) f(x)=log 2(128-124´ 2-|x|. Ответ: [2; 7) 4.1.4. Определить четные, нечетные функции и функции общего вида: а) д) Ответ: а) нечет.; б) чет.; в) общ. вида; г) нечет.; д) чет.; е) общ. вида; ж) нечет.; з) общ. вида; и) нечет. 4.1.5. Определяется ли заданная функция периодической; найти ее наименьший положительный период, если он существует: а) f(x)=sin 4 x; б) f(x)=cos2 5 x; в) f(x)=tg 4.1.6. Найти значение функции f (19), если известно, что функция f(x) нечетная, имеет период, равный 10, и на отрезке [0; 5] имеет вид у =25 х 2- х 4. Ответ: -24. 4.1.7. Построить графики функций: а) у = х 2-6 х +11; б) у =1 ______________ 4.1.8. Задана функция Найти Ответ: 4.1.9. Найти область определения функций D(f): а) г) Ответ: (-µ; 1)È (1; +µ); (-µ; +µ); (-µ; 1)È (3; +µ); [-2; 1); [-1; 3]; (-µ; +µ). 4.1.10. Найти множество значений функций E(f): а) f(x)=x2- 6 x +8; б) f(x)= 2-|x|; в) f(x)= 4+2 sin 5 x; г) д) Ответ: д) [0; 1]. 4.1.11. Установить, какие из следующих функций четные, нечетные, общего вида: а) f(x)=x 2+5 x 4; б) f(x)=xcosx; в) f(x)=tgx 2; г) f(x)= | x -2|. Ответ: а) чет.; б) нечет.; в) чет.; г) общего вида. 4.1.12. Найти значение функции f (22), если известно, что y=f(x) – нечетная функция с периодом 12 и на отрезке [0; 6] функция имеет вид у= 36 х 4- х 2. Ответ: -572. 4.1.13. Построить графики следующих функций: а) y=x 2-4 x -5; б) y=log 2(x- 1)+3; в)
|

 .
. .
. .
. ; б)
; б)  ; в) f(x)=log 3(9- x 2);
; в) f(x)=log 3(9- x 2); ; д)
; д) 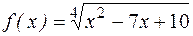 ; е)
; е)  .
. ; б) f(x)=x 4-5| x |; в) f(x)=ex- 2 e -x; г)
; б) f(x)=x 4-5| x |; в) f(x)=ex- 2 e -x; г)  ;
; ; е)
; е)  ; ж) f(x)=arcsinx; з) f(x)=xex; и)
; ж) f(x)=arcsinx; з) f(x)=xex; и)  .
. ; г) f(x)=sin 3 xcos 3 x; д)
; г) f(x)=sin 3 xcos 3 x; д)  .
. ; в) у =2х-1+3; г) у=log 2| x |; д) y= 3 cos 2 x.
; в) у =2х-1+3; г) у=log 2| x |; д) y= 3 cos 2 x. .
. .
. .
.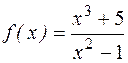 ; б)
; б)  ; в) f(x)=log2 (x2- 4 x +3);
; в) f(x)=log2 (x2- 4 x +3); ; д)
; д)  ; е) f(x)=tg 2 x.
; е) f(x)=tg 2 x. ;
; .
. .
.


