Разрывы функции
Функция f(x) имеет разрыв в точке а, если она определена слева, и справа от точки а, но в точке а не выполняется хотя бы одно из условий непрерывности. Различают два основных вида разрыва: 1. Разрывы I рода – а) оба односторонних предела существуют и конечны, но не равны между собой, то есть 2. Разрыв II рода – хотя бы один из односторонних пределов равен ±∞. _______________
4.2.1. Найти пределы следующих функций: а) Ответ: а) 7; б) 1; в) 1; г) 1. 4.2.2. Раскрыть неопределенность а) д) Ответ: а) -6; б) 1; в) 1/2; г) 4.2.3. Раскрыть неопределенность а) г) Ответ: а) 1/2; б) -5; в) 0; г) ∞; д) Ö 3. 4.2.4. Раскрыть неопределенности ∞ -∞ и 0∞: а) г) Ответ: а) 1, 5; б) 0, 5; в) 0; г) -2. 4.2.5. Вычислить пределы: а) д) з) Ответ: а) 4; б) 2; в) 4.2.6. Найти пределы: а) д) Ответ: а) е -5; б) е -1/3; в) е 4; г) е 2; д) е -2; ж) е 3. 4.2.7. Найти точки разрыва и построить графики функции: а) г) Ответ: а)II; б) II; в) II; г) I. 4.2.8. Подобрать значения a таким образом, чтобы функции были бы непрерывными: а) Ответ: а) a=1; б) не сущ. такого a. _________________
4.2.9. Найти пределы следующих функций: а) Ответ: а) 6; б) 0. 4.2.10. Раскрыть неопределенность а) г) Ответ: а) 2/5; б) 4/3; в) 1/20; г) 1, 6. 4.2.11. Раскрыть неопределенность а) г) Ответ: а) -1/4; б) 2; в) ∞; г) 1/2. 4.2.12. Раскрыть неопределенности ∞ -∞ и 0∞: а) Ответ: а)0; б)0; в)0; г)0. 4.2.13. Найти пределы: а) Ответ: а) 1/3; б) 8; в) -Ö 2; г) 2/5. 4.2.14. Найти пределы: а) Ответ: а) е 6; б) е -3/2; в) 1/ е 2; г) е. 4.2.15. Найти точки разрыва и построить графики функций: а) г) Ответ: а) II; б) I - устранимый; в) II; г) I – рода. 4.2.16. Найти a таким образом, чтобы следующие функции были непрерывными: а) Ответ: а) a=2; б) a=16/π.
|

 ≠
≠  . Такой разрыв называется скачком; б) оба односторонних предела существуют, конечны, равны между собой, но не равны значению функции в точке а, то есть
. Такой разрыв называется скачком; б) оба односторонних предела существуют, конечны, равны между собой, но не равны значению функции в точке а, то есть  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. и вычислить пределы:
и вычислить пределы: ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
; ; е)
; е)  .
. ; д) 2; е) -1/2.
; д) 2; е) -1/2. и найти пределы:
и найти пределы: ; б)
; б)  ; в)
; в)  ;
; ; д)
; д) 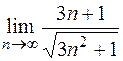 .
. ; б)
; б)  ; в)
; в)  ;
; .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
; ; е)
; е)  ; ж)
; ж)  ;
; .
. ; г) 1; д) -1/2; е) 2, 25; ж) 1; з) -8.
; г) 1; д) -1/2; е) 2, 25; ж) 1; з) -8. ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
; ; ж)
; ж)  .
. ; б)
; б)  ; в)
; в)  ;
; .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  ; в)
; в)  ;
; .
. ; б)
; б)  ; в)
; в)  ;
; .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. ; б)
; б)  ; в)
; в)  ;
; .
. ; б)
; б)  .
.


