Точки перегиба. Асимптоты
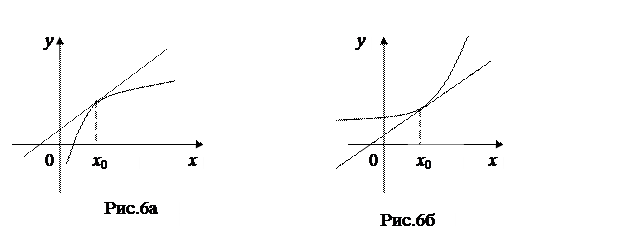
Кривая называется выпуклой в точке х=х 0, если в некоторой окрестности этой точки кивая расположена под касательной, проведенной в этой точке (рис.6а), если же кривая лежит над касательной, то функция называется вогнутой (рис.6б).
В качестве достаточных условий выпуклости, вогнутости графика функций можно принять следующие: если y" > 0, то кривая вогнутая, если y" < 0, то кривая выпуклая. Точкой перегиба называется точка, разделяющая интервал выпуклости от интервала вогнутости. Необходимым условием существования точки перегиба является равенство нулю второй производной от функции, достаточным – изменение знака второй производной при переходе через точку, подозрительную на точку перегиба. Пусть имеется кривая, ветвь которой в том или ином направлении удаляется в бесконечность. Если расстояние от точки кривой до некоторой прямой по мере удаления точки кривой в бесконечность стремится к нулю, то эта прямая называется асимптотой графика кривой. Существует три вида асимптот: вертикальная, горизонтальная, наклонная. Пусть y=f(x), а – точка разрыва функции или граничная точка области определения. Если Если Наклонная асимптота имеет вид у=kx+b, где Замечание. Пределы при х ®∞, х ®-∞ находятся отдельно.
Алгоритм полного исследования функции y=f(x)
1. Найти область определения функции; точки разрыва. 2. Найти асимптоты графика функции. 3. Определить четность, нечетность, периодичность функции. 4. Установить промежутки возрастания, убывания и экстремумы функции. 5. Определить интервалы выпуклости, вогнутости и точки перегиба графика функции. 6. Найти точки пересечения графика с осями координат. 7. При необходимости вычислить значения функции в дополнительных точках. ___________________
4.7.1. Найти промежутки выпуклости, вогнутости, точки перегиба: а) у=х 5-5 х -6; б) у=(х- 5 ) 5/3+2; в) у=хе х; г) у=х 4-8 х 3+24 х 2. Ответ: а) (-∞; 0) – выпуклая; (0; ∞) – вогнутая; б) р(5; 2) – точка перегиба; в) (-∞; -2) – выпуклая; (-2; ∞) – вогнутая; г) точек перегиба нет. 4.7.2. Найти асимптоты графика функций: а) в) Ответ: а) х =-2, у =3; б) х =1, х = -6, у =0; в) у=х -6; г) 4.7.3. Исследовать функции и построить их графики: а) в) Ответ: а) у min(2)=3; асимптоты у = х, х =0; б) у min(2Ö 3)=3Ö 3, у max(-2Ö 3)= -3Ö 3; (0; 0) – точка перегиба; х =±2, у=х – асимптоты; в) у max(е 2)=2/ е, у =0 – асимптоты; г) у max(1)= е. 4.7.4. Найти промежутки выпуклости, вогнутости, точки перегиба: а) в) y=ln|x|; г) Ответ: а) (2; -8/3); б) г) 4.7.8. Найти асимптоты графиков функций: а) в) Ответ: а) х= 0; у =1; б) 4.7.9. Исследовать функции и построить графики: а) Ответ: а) у=-х – наклонная асимптота; б) у min(6)=13, 5; (0; 0) – точка перегиба; х =2; у = х +4 – асимптоты.
|
, то прямая х=а есть вертикальная асимптота.
, то прямая х=b – горизонтальная асимптота.
; 
.
; б) 
;
; г) y=-xarctgx.
; б) 
;
; г) 
.
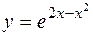; б) 
;
.
; в) точек перегиба нет;
.
; б) y=x-arctgx;
.
; в) у= 2 х; х =0.
; б) 
.
