Прямая и плоскость
Различным способам задания прямой в пространстве соответствуют разные виды ее уравнений, основные из которых представлены в таблице 5. Таблица 5
Пусть заданы две прямые своими каноническими уравнениями: l 1: l 2: Угол между прямыми определяется как Условие перпендикулярности прямых:
Условие параллельности прямых:
Пусть плоскость a задана уравнением А х +В у +С z +D=0, а прямая l – своими каноническими уравнениями
Условие параллельности прямой и плоскости А m +B n +C p =0. Условие перпендикулярности прямой и плоскости:
_____________
3.5.1. Написать канонические уравнения прямой, образующей с осями координат углы Ответ: 3.5.2. Написать канонические уравнения перпендикуляра, опущенного из начала координат на плоскость 4 х - у +2 z -3=0. Ответ: 3.5.3. Написать уравнения прямой, проходящей через точку М0(2; -3; -4) параллельно прямой: Ответ: 3.5.4. Написать уравнения прямой, проходящей через точку М0(2; 1; -1) перпендикулярно плоскости х-у+z+ 1=0. Ответ: 3.5.5. Найти угол между прямыми:
Ответ: p/3. 3.5.6. Доказать, что прямые
3.5.7. Написать уравнение плоскости, проходящей через пару параллельных прямых Ответ: 3 х -2 у -3=0. 3.5.8. Найти уравнение плоскости, проходящей через точку М0(1; -2; 3) и прямую: Ответ: 7 х +5 у -9 z +30=0. 3.5.9. Найти уравнение плоскости, проходящей через прямую Ответ: 6 х -5 у +3 z -11=0. 3.5.10. Найти точку пересечения Ответ: (3; 2; 7). 3.5.11. Найти угол между прямой Ответ: ________________
3.5.12. Написать уравнения прямой, проходящей через точки А(-1; 2; 3) и В(2; 6; -2). Найти ее направляющие косинусы. Ответ:
3.5.13. Написать уравнения прямой, проходящей через точку (-4; 3; 0) параллельно прямой Ответ: 3.5.14. Найти угол между прямыми Ответ:
3.5.15. Найти расстояние между прямыми Ответ: 3.5.16. Написать уравнение плоскости, проходящей через прямую Ответ: х -2 у + z +5=0. 3.5.17. Написать уравнение плоскости, проходящей через прямую Ответ: 8 х -5 у + z -11=0. 3.5.18. Написать уравнение плоскости, проходящей через прямые Ответ: х +2 у -2 z =1.
|


 называется направля-ющим вектором прямой
называется направля-ющим вектором прямой


 - уравнение одной плоскости;
- уравнение одной плоскости;
 - уравнение второй плоскости
- уравнение второй плоскости

 .
. .
. =0.
=0. .
. .
. .
. и проходящей через точку М0(-1; 0; 5).
и проходящей через точку М0(-1; 0; 5). .
. .
. .
. .
. .
. и
и  .
. и
и  параллельны.
параллельны. и
и  .
. .
. перпендикулярно плоскости 3 х +3 у - z +1=0.
перпендикулярно плоскости 3 х +3 у - z +1=0. с плоскостью 2 х +3 у -2 z +2=0.
с плоскостью 2 х +3 у -2 z +2=0. и плоскостью 6 х -3 у +2 z =0.
и плоскостью 6 х -3 у +2 z =0. .
.
 .
. .
.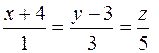 .
. и
и  .
. .
. и
и  .
. .
. и точку (3; 4; 0).
и точку (3; 4; 0). перпендикулярно плоскости 2 х +3 у - z =4.
перпендикулярно плоскости 2 х +3 у - z =4.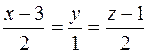 и
и 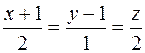 .
.


