Угол между двумя прямыми
Пусть прямые l 1 и l 2 заданы своими уравнениями с угловыми коэффициентами: l 1: y=k1х+b1, l2: y=k2x+b2, тогда острый угол между двумя прямыми определяется его тангенсом по формуле
Если прямые l 1 и l 2 заданы общими уравнениями А1 х +В1 у +С1=0 и А2 х +В2у+С2=0, то угол между ними можно найти как угол между их нормальными векторами
В случае задания прямых своими каноническими уравнениями
Условия параллельности и перпендикулярности прямых (Табл. 2) Таблица 2
|
.
.
угол между прямыми находится как угол между направляющими векторами прямых
.
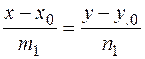l 2: 
