К каноническому виду
Общее уравнение кривой второго порядка имеет вид А х 2+2В ху +С у 2+2D х +2Е у +F=0, (1) где коэффициенты А, В, С одновременно в ноль не обращаются. С помощью преобразования системы координат уравнение (1) может быть приведено к простейшему (каноническому) виду. Если в уравнение (1) коэффициент В=0, то оно имеет вид А х 2+ С у 2 +2D х +2Е у +F=0. (2) К канонической форме уравнение (2) преобразуется с помощью параллельного переноса координатных осей по формулам
где (х 0; у 0) – координаты нового начала О’ системы координат относительно старой системы. Новые оси О’Х’, О’Y’ параллельны старым осям. После подстановки формул (3) в уравнение (2) выделяются полные квадраты по переменным х ’ и y ’. Если в уравнение (1) В≠ 0, то путем поворота координатных осей на некоторый угол a, определяемый формулой
можно исключить слагаемое, содержащее произведение текущих координат. Для этого необходимо подставить sina и cosa в формулы поворота координатных осей:
Затем следует выражение (5) подставить в уравнение (1). ______________
3.3.1. Привести к каноническому виду уравнение 4 х 2+5 у 2+20 х -30 у +10=0. Построить кривую. Ответ: 3.3.2. Преобразовать уравнение 3 х 2- Ответ: ________________
3.3.3. Привести к каноническому виду уравнение 5 х 2-4 у 2+16 у -36=0. Построить кривую. Ответ: 3.3.4. Привести к каноническому виду уравнение х 2+2 ху+у 2= Ответ: у = - х 2. _______________
|

 , (3)
, (3)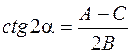 , (4)
, (4)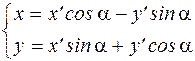 . (5)
. (5)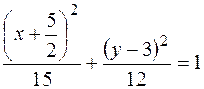 .
.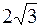 ху+у 2+6 х+
ху+у 2+6 х+ 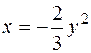 .
. .
.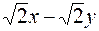 . Построить кривую.
. Построить кривую.


