Плоскость в пространстве
Любое уравнение первой степени в трехмерном пространстве определяет какую-либо плоскость. Разным способам задания плоскости соответствуют различные виды уравнений (табл. 4.) Таблица 4
Пусть даны две плоскости a1 и a2: a1: А1 х +В1 у +С1 z +D1=0, a2: А2 х +В2 у +С2 z +D2=0.
Угол между двумя плоскостями определяется как Условие перпендикулярности двух плоскостей:
Условие параллельности двух плоскостей:
Расстояние от точки до плоскости:
где А х +В у +С z +D=0 – заданная плоскость; М(x 0, y 0, z 0) – данная точка. _________________
3.4.1. Написать уравнение плоскости, проходящей через точку М(-1; 2; 3) перпендикулярно вектору Ответ: х -2 у -3 z +14=0. 3.4.2. Написать уравнение плоскости, проходящей через точки М1(2; 3; -1), М2(1; 5; 3) перпендикулярно плоскости 3 х - у +3 z +15=0. Ответ: 2 х +3 у - z -14=0. 3.4.3. Написать уравнение плоскости, проходящей через точку М0(-2; 7; 3) параллельно плоскости х -4 у +5 z +1=0. Ответ: х -4 у +5 z +15=0. 3.4.4. Написать уравнение плоскости, проходящей через точку М0(2; -3; 1) параллельно векторам Ответ: х + у - z +2=0. 3.4.5. Написать уравнение плоскости, проходящей через точку М0(2; 2; -2) перпендикулярно линии пересечения плоскостей 3 х -2 у - z +1=0 и х - у - z =0. Ответ: х +2 у - z -8=0. 3.4.6. Написать уравнение плоскости, проходящей через точки М1(3; -1; 2), М2(4; -1; -1), М3(2; 0; 2). Ответ: 3 х +3 у + z -8=0. 3.4.7. Написать уравнение плоскости, проходящей через ось ОZ и точку М0(1; -2; 1). Ответ: 2 х + у =0. 3.4.8. Написать уравнение плоскости, проходящей через точку М0(2; 3; -4) параллельно плоскости YOZ. Ответ: х -2=0. 3.4.9. Найти расстояние от точки М1(2; -1; -1) до плоскости 16 х- 12 у +15 z -4=0. Ответ: 1. 3.4.10. Найти угол между плоскостями х + у -1=0 и 2 х - у + Ответ: _______________
3.4.11. Даны точки М1(0; -1; 3), М2(1; 3; 5). Написать уравнение плоскости, проходящей через точку М1 перпендикулярно вектору Ответ: х+ 4 у +2 z -2=0. 3.4.12. Написать уравнение плоскости, проходящей через точки (0; -5; 0) и (0; 0; 2) перпендикулярно плоскости х+ 5 у +2 z -10=0. Ответ: 2 у -5 z +10=0. 3.4.13. Написать уравнение плоскости, проходящей через точку М0(-2; 1; 4) параллельно плоскости 3 х+ 2 у -7 z +8=0. Ответ: 3 х+ 2 у -7 z +32=0. 3.4.14. Написать уравнение плоскости, проходящей через точку М0(-2; 3; 6) перпендикулярно плоскостям 2 х+ 3 у -2 z -4=0, 3 х+ 5 у + z =0. Ответ: 13 х- 8 у + z +44=0. 3.4.15. Написать уравнение плоскости, проходящей через три точки М1(1; -1; 0), М2(2; 1; -3), М3(-1; 0; 1). Ответ: х + у + z =0. 3.4.16. Найти угол между плоскостями х+ 2 у -3 z +4=0, 2 х+ 3 у + z +8=0. Ответ: 3.4.17. Найти расстояние от точки М0(1; 3; -2) до плоскости 2 х- 3 у -4 z +12=0. Ответ:
|

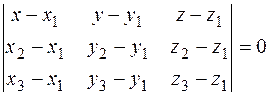

 .
. =0, то есть
=0, то есть 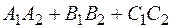 =0.
=0.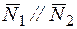 или
или 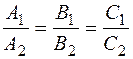 .
. ,
,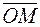 .
.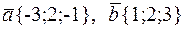 .
. z +1=0.
z +1=0. .
.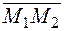 .
. .
.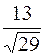 .
.


