Кривизна плоской кривой
Пусть даны две функции переменной величины Если Пусть теперь некоторая кривая задана в пространстве R3 своими параметрическими уравнениями: Если
Пусть задана плоская кривая уравнением y=f(x). Величина Радиус кривизны есть ________________
4.8.1. Найти Ответ: 4.8.2. Исключить параметр t из уравнений x=acost, y=bsint. Построить кривую. Ответ: 4.8.3. Траектория движения материальной точки задана уравнением Ответ: 4.8.4. Определить кривизну кривой Ответ:
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Бугров, Я.С. Высшая математика. Элементы линейной алгебры и аналитической геометрии: учеб. для вузов./ Я.С. Бугров, С.М. Никольский. – М.: Дрофа, 2003. 2. Бугров, Я.С. Высшая математика. Дифференциальное и интегральное исчисление: учеб. для инж.-техн. спец. вузов./ Я.С. Бугров, С.М. Никольский. – М.: Дрофа, 2005. 3. Письменный, Д.Т. Конспект лекций по высшей математике / Д.Т. Письменный. – 2-е изд. – М.: Астрис-пресс, 2003. – Ч.1. 4. Минорский, В.П. Сборник задач по высшей математике: учеб. пособие для втузов/ В.П. Минорский. – М: физ.мат.лит., 2004. 5. Данко, П.Е. Высшая математика в упражнениях и задачах. /П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М.: Оникс 21 век; Мир и образование, 2005. – Ч.1.
|

 , рассматриваемые для одних и тех же значений t. Эти уравнения на плоскости задают некоторую кривую. Так как переменная t называется параметром, то и приведенная система называется параметрическим уравнением кривой.
, рассматриваемые для одних и тех же значений t. Эти уравнения на плоскости задают некоторую кривую. Так как переменная t называется параметром, то и приведенная система называется параметрическим уравнением кривой. , то
, то  , а
, а  .
.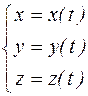 . Тогда каждому значению t можно поставить в соответствие вектор
. Тогда каждому значению t можно поставить в соответствие вектор  , который называется векторной функцией скалярного аргумента t. Линия с, описываемая концом радиуса – вектора
, который называется векторной функцией скалярного аргумента t. Линия с, описываемая концом радиуса – вектора  , называется годографом.
, называется годографом.
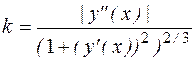 определяет ее кривизну.
определяет ее кривизну. . Для параметрически заданной кривой
. Для параметрически заданной кривой  .
. , если x=arccost, y=arcsint.
, если x=arccost, y=arcsint. .
. .
. . Найти закон изменения скорости движения. Построить траекторию и векторы скорости при t =0; t =1.
. Найти закон изменения скорости движения. Построить траекторию и векторы скорости при t =0; t =1.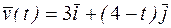 .
. при t =1.
при t =1. .
.


