Энергия электрического поля заряженного плоского конденсатора
где V = S× d - объем пространства между обкладками конденсатора; E - напряженность электрического поля; d - расстояние между пластинами конденсатора; S - площадь одной из пластин конденсатора. Объемная плотность энергии однородного электрического поля – энергия единицы объема электрического поля:
Объемная плотность энергии однородного электрического поля в диэлектрике
где слагаемое слагаемое Энергия электрического поля (в том числе и неоднородного)
Механические силы, действующие на макроскопические заряженные тела:
3.5. Основные уравнения электростатики в вакууме: а) закон сохранения заряда в интегральной форме:
где r - объемная плотность заряда; j - вектор плотности тока; б) закон сохранения заряда в дифференциальной форме:
в) дифференциальная запись закона Кулона:
г) теорема Остроградского - Гаусса для непрерывного распределения зарядов:
д) дифференциальное уравнение потенциальности электростатического поля: rot E = 0; (3.86) г) уравнение Пуассона: Dj = r/e0, (3.87) где д) уравнение Лапласа: Dj = 0; (3.88) е) формула Стокса:
3.6. Основные уравнения электростатики диэлектриков: 1) условие нейтральности объема:
|
, (3.77)
. (3.78)
, (3.79)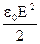
- объемная плотность энергии электрического поля в вакууме;
- объемная плотность энергии электрического поля, затраченная на поляризацию диэлектрика.
. (3.80)
. (3.81)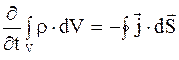
, (3.82)
; (3.83)
; (3.84)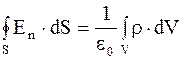
; (3.85)
- оператор Лапласа;
. (3.89)
; (3.90)
