Случайное событие и вероятность
Основные положения теории вероятностей являются аппаратом теории информации. Существует связь между абстрактным понятием вероятности и частотой случайного события в результате некоторого эксперимента (опыта). Под случайными событиями принимаются события, которые могут произойти или не произойти в результате данного опыта. Если при N-кратном повторении какого-либо опыта относительное число появлений ni -го события по мере увеличения общего числа реализаций этого опыта N стремится к некоторому пределу:
то говорят о статистической устойчивости результатов данного опыта. Числа Рi, позволяющие при этом количественно сравнивать события по степени их возможности, называются вероятностями этих событий. Чем чаще имеет место данный исход опыта, тем больше его вероятность. События подразделяются на достоверные (U), невозможные (V) и случайные (А1, А2, А3, … или А, В, С …). Достоверное событие, которое непременно должно произойти при каждом испытании, имеет максимально возможное значение вероятности P(U)=1. В противоположность ему невозможное событие, т.е. событие, которое в данном опыте не может произойти, имеет минимальное значение вероятности P(V)=0. Для всех остальных событий, которые могут иметь место при данном опыте, но не при каждом его повторении, вероятность лежит в пределах:
Для некоторых опытов вероятности отдельных исходов могут быть предсказаны умозрительно на основе анализа условий опыта. Это, как правило, те случаи, когда можно выделить такие элементарные исходы опыта, ни одному из которых нельзя отдать предпочтение, так что все они должны приниматься равновероятными. Так, например, при бросании монеты нет никаких оснований отдать предпочтение одному из двух возможных исходов опыта (падение монеты гербом вверх или вниз) и обеим им должна приписываться одинаковая вероятность, равная 1/2. То же относится и к бросанию игральной кости в виде идеального кубика, когда любая из его граней с одинаковой вероятностью Рi = 1/6 может оказаться верхней. Нет оснований отдать предпочтение и какой-либо из игральных карт при их сдаче из хорошо перетасованной колоды и т.д. В более сложных случаях, когда не удается умозрительно определить вероятности элементарных исходов опыта, единственным методом их определения остается непосредственный подсчет относительной частности появления отдельных исходов при многократном воспроизведении опыта. В этом случае опыт одновременно позволяет убедиться в статистической устойчивости его результатов и найти вероятности отдельных исходов. В большинстве случаев, представляющих практический интерес, мы сталкиваемся со сложными событиями, представляющими определенные сочетания исходов ряда элементарных опытов. Прибегать для оценки вероятности такого сложного события каждый раз к опыту чрезвычайно трудно, а иногда и просто невозможно (например, при проектировании, когда объект испытаний вообще отсутствует). Возникает задача косвенной оценки вероятности сложных событий через известные вероятности других событий, логически с ними связанных. Систему таких косвенных методов оценки вероятностей, позволяющих свести к минимуму экспериментальной оценки, дает теория вероятностей. Введем некоторые понятия, являющиеся основополагающими для теории вероятностей. События называются несовместными (или несовместимыми) в данном опыте, если никакие два из них не могут появиться вместе. Если в результате каждой конкретной реализации опыта обязательно должно появиться хотя бы одно из событий А1, А2 …..Аn, то такая группа событий называется полной. Два события называются противоположными (дополнительными), если они несовместны и образуют полную группу. Событие, противоположное событию А, обозначается Ā Нахождение противоположного события эквивалентно логической операции НЕ (отрицания), иными словами Ā = не А. События называются независимыми, если вероятность появления одного из них не зависит от того, имело место или нет другое из этих событий. Если же вероятность события А зависит от того, имело ли место событие В, то такие события называются зависимыми. В этом случае можно ввести условную вероятность Р(А|В), представляющую вероятность события А при условии, что имело место событие В. Суммой или объединением множества событий А1, А2, А3, … называется такое событие А, которое происходит по крайней мере одно («хотя бы одно») из этих событий. Сумма событий А1, А2, А3, … обозначается:
Или
где Из определения суммы событий непосредственно вытекают следующие соотношения: А + А = А, А + U = U, A + V = A, A + B = B + A, (A + B) + C = A + (B + C). Произведением (или пересечением, или совмещением) событий А1, А2, А3, … называется такое событие А, которое происходит тогда и только тогда, когда происходят все события вместе («одновременно »). Для обозначения произведения событий применяются следующие записи:
Или
где ∩ - символ пересечения событий (логическая операция И). Для произведения событий справедливы соотношения: АА = А, AV = V, AU = A, AB = BA, (AB)C = A(BC) Понятия суммы и произведения употребляются здесь не в арифметическом смысле, а обозначают соответствующие логические операции. В основе косвенных методов оценки вероятности сложного события А через вероятности более простых событий А1, А2, …Аn базируется на использовании основных теорем теории вероятностей (теорем сложения и умножения вероятностей и их следствий). Согласно теореме сложения вероятностей вероятность суммы двух событий равна сумме вероятностей этих событий минус вероятность их произведения:
Если события А и В несовместимы, то:
Формулы (2.3) и (2.4) обобщаются на сумму любого числа n событий:
Сумма вероятностей несовместимых событий, составляющих полную группу, равна единице:
Сумма вероятностей двух противоположных событий равна единице:
По теореме умножения вероятностей для двух событий вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что произошло первое:
где P (A|B) - условная вероятность события А, т.е. вероятность события А, вычисленная в предположении, что имело место событие В. Если событие А статически не зависит от события В, то P (A|B) = P(A), причем события А и В называются независимыми. При независимых событиях А и В выражение (2.9) принимает вид:
Формулы (2.9.) и (2.10.) обобщаются на n событий А1, А2, …Аn:
Решение многих практических задач требует совместного использования теорем сложения и умножения вероятностей. В частности, с помощью этих теорем производится расчет вероятности безотказной работы, например, радиотехнических систем. Из формулы (2.9.) получаем:
Решение многих практических задач требует совместного использования теорем сложения и умножения вероятностей в частности с помощью этих теорем производится расчет вероятностей безотказной работы, например систем передачи информации. Найдем вероятность Рn, k того, что при n независимых испытаниях, исходом которых может быть одно из двух противоположных событий А или Ā;, событие А произойдет ровно k раз. Вероятность события А обозначим Р(А) = Р, тогда Р(Ā) = 1 – Р. Вероятность конкретной комбинации исходов n независимых испытаний, когда при определенных k испытаниях появилось событие А, а при остальных n – k испытаниях – событие Ā, в соответствии с теоремой умножения вероятностей равна Pk (1 – P)n – k, независимо от того, в каком порядке чередовалисьв данной комбинации исходы событий А и Ā;. Интересующее нас сложное событие представляет сумму всех исходов n-кратных испытаний, дающих k появлений события А. Поскольку исходы с разным порядком чередования событий А и Ā несовместны, а число исходов, дающих в разной последовательности k появлений события А в n испытаниях, равно числу сочетаний из n элементов по k, то в соответствии с теоремой сложения вероятностей
(При решении многих задач целесообразно использовать «комбинаторные» способы, т.е. теорию Соединений (размещений, перестановок, сочетаний). В формуле (2.12)
Во многих реальных ситуациях то или иное событие А может появляться лишь как случайное следствие одного из несовместных событий Hi (i= 1, 2, …, n), которые входят в некоторую полную группу событий и называются гипотезами. В таких случаях безусловная вероятность P (A) события A при известных вероятностях гипотез P (Hi) и условных вероятностях P (A|Hi) определяется по формуле полной (или средней) вероятности:
При этих же данных, т.е. известных вероятностях P (Hi) и P (A|Hi), можно найти изменение вероятностей гипотез Hi, если предположить, что событие A уже произошло. Задачи подобного типа решаются с помощью теоремы гипотез (или формулы Байеса):
Вероятность P (Hi) называется априорной (доопытной), а P (A|Hi) – апостериорной (послеопытной), обратной вероятностью, или функцией правдоподобия той или иной гипотезы об исходе непосредственно не наблюдаемого явления H при известном исходе явления A, если только известны значения вероятностей P (Hj) исходов Hj (в сочетании с любым из исходов Аi) и значения условных вероятностей P (Ai|Hj).
|

 (2.1)
(2.1) (2.2)
(2.2)

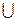 - символ объединения событий (логическая операция ИЛИ).
- символ объединения событий (логическая операция ИЛИ).

 (2.3)
(2.3) (2.4)
(2.4) (2.5)
(2.5) (2.6)
(2.6) (2.7)
(2.7) (2.8)
(2.8) (2.9)
(2.9) (2.10)
(2.10) (2.9а)
(2.9а)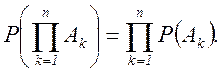 (2.10а)
(2.10а)
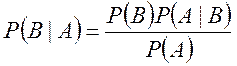 (2.11)
(2.11) (2.12)
(2.12) – число сочетаний из n элементов по k. Формула (2.12) носит название биноминального закона.
– число сочетаний из n элементов по k. Формула (2.12) носит название биноминального закона. (2.13)
(2.13) (2.14)
(2.14)


