Корреляционные характеристики случайных процессов
При рассмотрении случайных величин наряду с законами распределения весьма полезными оказались некоторые числовые характеристики (среднее значение, дисперсия, и др.), представляющие детерминированные величины. При рассмотрении случайных процессов аналогичную роль играют, детерминированные функции, дающие те же числовые характеристики случайных величин, представляющих значения этих процессов в соответствующих временных сечениях. К числу таких характеристик относятся среднее значение, дисперсия, корреляционная функция случайного процесса и др. Среднее значение или первый начальный момент случайного процесса ξ (t) представляют функцию времени
где ω 1(x; t) – одномерное распределение случайной величины, представляющей возможные значения случайного процесса ξ (t) в фиксированный момент времени t. Дисперсия случайного процесса ξ (t) и 2-й центральный момент также представляет функцию времени
Корреляционная функция случайного процесса или смешанный 2-й начальный момент представляет двумерную функцию времени
где ω 2(x1, x2; t1, t2) – двумерное распределение случайных величин ξ (t1) и ξ (t2), представляющих возможные значения случайного сигнала ξ (t) для временных сечений t1 и t2. Часто вместо случайного процесса рассматривают его флюктуации – отклонения от среднего значения
Нетрудно видеть, что aξ 0(t)=0, а Корреляционная функция флуктуации случайного процесса носит название ковариационной функции и имеет вид
Из (2.31) и (2.28) следует, что
т.е. дисперсия представляет значение ковариационной функции Случайный процесс ξ (t) называется строго стационарным или стационарным в «узком смысле», если его функция распределения ω n(x1, x2, …, xn; t1, t2, …, tn) произвольного порядка n не меняется при любом сдвиге всей группы точек t1, t2, …, tn, т.е. при соблюдении для любых n и τ условия:
Из (2.32) следует, что двумерная функция распределения стационарного процесса зависит только от интервала τ =t2 – t1 между точками отсчета:
а одномерная функция распределения ω 1(x) не зависит от временного сечения. Соответственно для стационарного случайного процесса от начала отсчета времени не зависит и введенные статистические характеристики
Следует заметить, что условие (2.33) и вытекающие из него условия (2.34) – (2.36) являются необходимыми, но недостаточными условиями строгой стационарности случайного процесса, ибо независимость от начала отсчета времени двумерной функции распределения еще не гарантирует соблюдение этого же условия и для всех распределений более высокого порядка, т.е. выполнения условия (2.32) при любом n. Однако для большого числа практических задач оказывается достаточным знание свойств процессов, определяемых первыми двумя моментами. Раздел теории, посвященный изучению этих свойств, называется корреляционной теорией. В рамкахкорреляционной теории процессы, удовлетворяющие условию (2.33), ничем не отличаются по своим свойствам от строго стационарных. Случайные процессы, удовлетворяющие этому условию, получили название стационарных в широком смысле слова (или в смысле Хинчина). Мы будем рассматривать именно такие процессы и будем называть их для краткости просто стационарными. Корреляционная и ковариационная функция стационарного случайного процесса, описываемого действительной функцией времени, обладают следующими свойствами: 1) являются четными функциями аргумента τ
2) при τ =0 имеют максимальное значение, равное соответственно 3) при τ → ∞ Нормированной корреляционной функцией (коэффициентом корреляции) называется функция
Очевидно, что ρ ξ (0)=1 и ρ ξ (∞)=0. Из последнего условия следует, что для стационарного случайного процесса, как правило, можно выбрать такое значение τ 0, что при τ > τ 0 корреляцией между отсчетами процесса можно пренебречь. Поскольку максимальное значение |ρ ξ (τ)| равно 1, то в качестве меры скорости спада |ρ ξ (τ)|, т.е. меры интервала τ 0, при значительном превышении которого можно не считаться с корреляцией между отсчетами, можно использовать площадь под кривой |ρ ξ (τ)|, приняв
(Практически корреляцией можно пренебречь уже при τ ≥ (3 – 4)τ 0.). Величина τ 0, определяемая формулой (2.38), называется интервалом корреляции. Геометрически интервал корреляции может интерпретироваться как половина ширины прямоугольника единичной высоты, площадь которого равновелика площади, ограничиваемой кривой |ρ ξ (τ)| (рис. 2.3).
Рис. 2.3 Случайный процесс называется эргодическим, если любая его статистическая характеристика, полученная усреднением по множеству возможных реализаций, с вероятностью, сколь угодно близкой к единице, равна соответствующему временному среднему, полученному на достаточно большом интервале времени из одной единственной реализации случайного процесса. Эргодичность случайного процесса предполагает его стационарность, но не наоборот: стационарный процесс может не быть эргодическим. Например, случайный процесс вида
где ξ 0(t) – эргодический случайный процесс; η – случайная величина, меняющаяся от реализации к реализации, будет стационарным, но не эргодическим (его числовые характеристики, полученные осреднением по времени, меняются от реализации к реализации из-за изменения η). Если случайный процесс эргодический, то любая его достаточно длительная реализация представляет свойства всей совокупности. Начальный момент k -го порядка для такого процесса и его корреляционная функция удовлетворяют условиям:
для любой r -й реализации процесса. Эргодичность процесса создает большие удобства для опытного определения статистических характеристик, так как позволяет получить их из одной достаточно длительной реализации случайного процесса.
2.5 Контрольные вопросы к разделу 2 в форме «Задание – тест». 1. События, которые могут произойти или не произойти в результате денного опыта, называются:
|

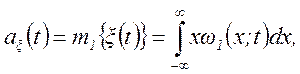 (2.27)
(2.27) (2.28)
(2.28) (2.29)
(2.29) (2.30)
(2.30)
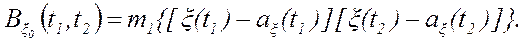 (2.31)
(2.31)
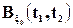 при равенстве аргументов t1 и t2.
при равенстве аргументов t1 и t2. (2.32)
(2.32) (2.33)
(2.33) (2.34)
(2.34) (2.35)
(2.35) (2.36)
(2.36) ;
;  ;
; и
и  ;
; , а
, а  .
.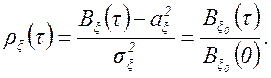 (2.37)
(2.37)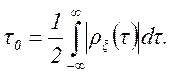 (2.38)
(2.38)
 (2.39)
(2.39) (2.40)
(2.40)



