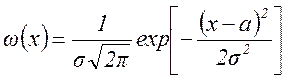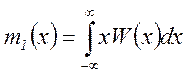Дифференциальный; 2) интегральный; 3) числовой
17. Особое место среди вероятностных характеристик случайных величин занимает нормальный дифференциальный закон распределения (плотность вероятностей)
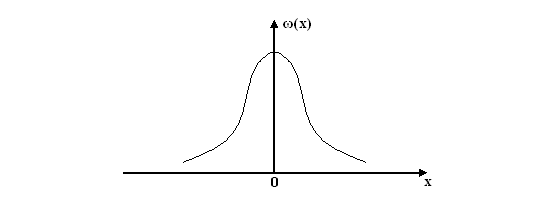
(где σ 2 – дисперсия, а – среднее значение, σ – среднеквадратическое отклонение) представлен на рис. 2.4, для a = 0
Рис. 2.4. Значение интегральной функции распределения
при x1=0, x2=∞ равно: 1) 1; 2) 0, 5; 3) 0. 18. при x1=-∞, x2=+∞ равно: 1) 0; 2) 0, 5; 3) 1. 19. при x1=-∞, x2=0 равно: 1) 1; 2) 0; 3) 0, 5.
20. Числовая характеристика случайной величины x, определяемая как начальный момент 1-порядка по формуле
(где ω (x) плотность вероятностей) называют: Среднеквадратическое отклонение; 2)среднее значение; Дисперсия. 21. Числовая характеристика случайной величины x определяемая как центральный момент 2-го порядка по формуле:
(где m1(x) – среднее значение, ω (x) – плотность вероятностей) называют: Среднеквадратическое отклонение; 2) среднее значение;
|