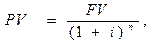Текущая стоимость денег
Процедура расчета текущей (приведенной) стоимости денег противоположна вычислению будущей стоимости. С ее помощью мы можем определить, какую сумму необходимо вложить сегодня для того, чтобы получить определенную сумму в будущем. Общая формула для вычисления приведенной стоимости 1 руб. через n периодов имеет вид:
где PV – текущая стоимость денег, FV – будущая стоимость денег, n – количество временных интервалов, i – ставка дисконтирования. Пример. Какую сумму необходимо положить на счет, чтобы через пять лет получить 1000 руб. (i=10%) PV = 1000 / (1+0.1)^5 = 620.92 руб. Таким образом, для расчета текущей стоимости денег мы должны известную их будущую стоимость поделить на величину (1+i)n . Текущая стоимость находится в обратной зависимости от величины ставки дисконтирования. Например, текущая стоимость денежной единицы, получаемой через 1 год при ставке 8% составляет PV = 1/(1+0, 08)1 = 0, 93, А при ставке 10% PV = 1/(1+0, 1)1 = 0, 91. Текущая стоимость денег находится также в обратной зависимости от числа временных периодов до их получения. Рассмотренная процедура дисконтирования денежных потоков может быть использована при принятии решений об инвестировании. Наиболее общее правило принятия решений – правило определения чистой приведенной стоимости (NPV). Суть его состоит в том, что участие в инвестиционном проекте целесообразно в том случае, если приведенная стоимость будущих денежных поступлений от его реализации превышает первоначальные инвестиции. Пример. Имеется возможность купить сберегательную облигацию номиналом 1000 руб. и сроком погашения 5 лет за 750 руб. Другим альтернативным вариантом инвестирования является размещение денег на банковском счету с процентной ставкой 8% годовых. Необходимо оценить целесообразность инвестирования средств в приобретение облигации. Для расчета NPV в качестве процентной ставки или в более широком смысле ставки доходности, необходимо использовать альтернативную стоимость капитала. Альтернативная стоимость капитала – это та ставка доходности, которую можно получить от других направлений инвестирования. В нашем примере альтернативным видом инвестирования является помещение денег на депозит с доходностью 8%. Сберегательная облигация обеспечивает денежные поступления в размере 1000 руб. через 5 лет. Текущая стоимость этих денег равна PV = 1000/1.08^5 = 680.58 руб. Таким образом, текущая стоимость облигации составляет 680.58 руб., в то время как купить ее предлагают за 750 руб. Чистая текущая стоимость инвестиций составит 680.58-750=-69.42, и инвестировать средства в приобретение облигации нецелесообразна. Экономический смысл показателя NPV состоит в том, что он определяет изменение финансового состояния инвестора в результате реализации проекта. В данном примере в случае приобретения облигации богатство инвестора уменьшится на 69.42 руб. Показатель NPV может быть также использован для оценки различных вариантов заимствования денежных средств. Например, вам нужно взять в долг 5000 дол. для приобретения автомобиля. В банке вам предлагают заем под 12 % годовых. Ваш друг может одолжить 5000 дол., если вы отдадите ему 9000 дол. через 4 года. Необходимо определить оптимальный вариант заимствования. Рассчитаем текущую стоимость 9000 дол. PV = 9000/(1+0.12)^4 = 5719.66 дол. Таким образом, NPV данного проекта составляет 5000-5719.66= -719.66 дол. В данном случае лучшим вариантом заимствования является банковский кредит. Для расчета эффективности инвестиционных проектов можно использовать также показатель внутренней нормы доходности (internal rate of return) IRR. Внутренняя ставка доходности – это такое значение дисконтной ставки, которое уравнивает приведенную стоимость будущих поступлений и приведенную стоимость затрат. Другими словами, IRR равна процентной ставки, при которой NPV = 0. В рассмотренном примере приобретения облигации IRR вычисляется из следующего уравнения 750 = 1000/(1+IRR)^5 IRR = 5.92%. Таким образом, доходность облигации при ее погашении составляет 5.92% в год, что существенно меньше доходности банковского депозита.
|