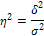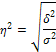Корреляция қатынасы

Қ оғ амдык қ ұ былыстар мен процестердің ө згеруін жә не бір-біріне тә уелділігін, яғ ни нә тижелі белгі мен факторлы белгі арасындағ ы байланыс тығ ыздығ ын зерттейтін бірден-бір кө рсеткіш - корреляциялық қ атынас ә дісі. Бұ л ә діс тә уелділіктің тү зу немесе қ исық сызық тығ ына карамастан барлык жағ дайда қ олданылады жә не одан шық қ ан кө рсеткіш байланыс тығ ыздығ ын дә л кө рсетеді.

Корреляция қ атынасы деп қ атысты шаманы айтады жә не оны математикалық статистикада гректің η (эта) ә рпімен белгілейді. Мұ нда шашыранды қ осындысының ережесін (σ ²=δ ²+ )негізге ала отырып, топаралық шашырандының (δ ^г) жалпы шашырандығ а (σ ²) қ атынасы қ арастырылады, оны ғ ылымда тө мендеу (детерминация) коэффициенті деп атайды. Тө мендеу коэффициенті тө мендегі формула бойынша есептеледі:

мұ нда η ²- тө мендеу (детерминация) коэффициенті;

δ ² - факторлы белгінің (топаралык) шашырандысы;

σ ² - нә тижелі белгінің (жалпы) шашырандысы.

Егер осы берілген формуланы шаршы тү бірге алатын болсақ, онда корреляция индексі немесе корреляциялық қ атынасы анық талады, яғ ни топтық пен қ орытындылаушы белгілердің арасындағ ы тығ ыз байланысты байқ ауғ а мү мкіндік туады, факторлық белгілердің нә тижелі белгілерге тигізген ә серін сипаттайды.Ол тө мендегі формула бойыншаесептеледі:

Корреляциялы қ атынастың мә ні ә рдайым нө л мен бірдің арасындағ ы кез-келген мә нде болуы мү мкін. Егер х пен у мә ндерінің арасында байланыс жоқ десек, онда корреляциялық қ атынас нө лге (σ = 0), ал керісінше х пен у арасында тү зу сызық ты байланыс бар болса, онда корреляциялық қ атынас бірге [η = 1) тең болады. Корреляциялық қ атынастың мә ні неғ ұ рлым жоғ ары, яғ ни бірге жақ ын болса, соғ ү рлым нә тижелі белгі мен факторлы белгінің арасында тү зу сызық ты тығ ыз байланыстың бар екендігі кө рінеді.

Корреляциялық қ атынас кө рсеткіштерінін негізінде байланыс тығ ыздығ ының сапалылығ ын бағ алау ү шін американ ғ алымы Чэддоктың ұ сынғ ан кестесін қ олданғ ан жө н, ол тө мендегідей:

Есептелген корреляция коэффициенттеріне осы берілген кесте кө рсеткіштері аркылы толық сипаттама беруге болады, бұ л байланыс кү шін анық тауғ а кө мектеседі.[53]