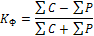Рангілі және Фехнер коэффициенттері

Факторлык белгі (х) мен нә тижелі белгі (у) шамаларының арасындағ ы байланыс тығ ыздығ ын есептеу кезінде тү рлі қ иындық ка кездесеміз жә не есептеу кө лемі ұ лғ аяды. Сондық тан, ө згермелі осы екі белгінің арасындағ ы байланыс тығ ыздығ ын анық тау ү шін жең ілдетілген жай тә сілді қ олданамыз. Осындай ең кө п тарағ ан тә сіл тү ріне рангілі корреляция коэффициенті жатады, кейде оны Спирмэннің коэффициенті деп те атайды.

Статистикада бұ л коэффициентті гректің «ро» (Р) - ә рпімен белгілейді жә не тө мендегі формула бойынша есептейді:

мұ нда d²- х пен У мэндерінің рангілері арасындағ ы айырмашылық (d=N_x-N_y) п - қ атардың саны.

Бұ л кө рсеткішті есептеу ү шін факторлық (х) жә не нә тижелі (у) белгі мә ндері ө су немесе кему дә режесі бойынша рангіленеді, яғ ни жиынтық тың ә рбір бірліктері ө здеріне тә н белгілеріне қ арай ретке келтіріледі жә не жеке нө мірленеді.

Егер х пен у -тің ө згермелі мә ндері бірдей шамалармен берілген болса, онда олардың рет нө мірінің қ осындысын екіге бө лу арқ ылы орташа шамасы табылады да, ә ркайсысы ретіне қ арай жеке нө мірленеді.

Жалпы алғ анда, рангілі корреляция коэффициенті ә рқ ашанда нө лден (0) плюс-минус бірге дейін (±1) ө згереді жә не оны кез келген сандар қ атары бойынша есептеуге мү мкіндік туады.

Натижелі жә не факторлық белгілер арасың дағ ы байланыс тығ ыздығ ын шашыранды мен корреляциялық талдау ә дісін қ олдану арқ ылы зерттеу жү ргізу белгілі бір киындық ка алып келеді жә не есептеу жұ мыстарының кө лемін кө бейтеді. Соң дық тан бұ лардың арасындағ ы байланыс тығ ыздығ ын жуық шамамен сипаттайтын есептеу жұ мыстары аздау жә не ең қ арапайым тү рі болғ ан таң балы корреляция коэффициенті есептеледі, оны Фехнер коэффициенті деп те атайды.

Егер ауытқ у белгілеріне сә йкес келуін С - ә ріпмен, ал сә йкес келмеуін Р - ә рпімен белгілейтін болсақ. онда Фехнер коэффициентін тө мендегі формула арқ ылы есептеуге болады: [51]