Булеан бесконечного множества. Выводы
Мы показали, что несчетные множества имеют мощность большую, чем счетные. А существуют ли множества наибольшей мощности? На этот вопрос отвечает теорема, на основании которой мы можем утверждать, что не существует множества наибольшей мощности: для каждого множества X мы можем построить его булеан, т.е. множество большей мощности. Это означает, что ряд мощностей (рис. 1.25) неограничен. Теорема. Пусть X – бесконечное множество. Мощность булеана множества X больше мощности множества X. Доказательство. Очевидно, что мощность булеана B (X) не меньше мощности множества X: булеан имеет подмножество одноэлементных множеств, равномощное множеству X. Остается показать, что Предположим противное: пусть Действительно, пусть такой элемент Случай а) невозможен, т.к. Следовательно, предположение о равномощности множеств X и Итак, используя понятие “мощность”, мы сравниваем между собой не только конечные, но и бесконечные множества. Мощность – это то общее, что есть у всех равномощных множеств, а общим у них является класс эквивалентности. Мы говорим, что множество имеет мощность À 0, и это означает, что оно принадлежит тому же классу эквивалентности, что и множество натуральных чисел; мы говорим, что множество имеет мощность континуума, и это означает, что оно принадлежит тому же классу, что и отрезок [0; 1] (табл. 1.5). Другие классы бесконечных множеств используются реже, чем счетные и несчетные. Таблица 1.5 Мощность множества
|

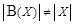 .
.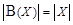 . Это означает, что существует биекция
. Это означает, что существует биекция 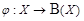 , т.е. каждый элемент x множества X имеет единственный прообраз
, т.е. каждый элемент x множества X имеет единственный прообраз 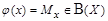 , а каждый элемент булеана имеет единственный прообраз во множестве X. Рассмотрим множество
, а каждый элемент булеана имеет единственный прообраз во множестве X. Рассмотрим множество 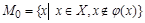 . Покажем, что множество
. Покажем, что множество 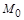 хотя и принадлежит булеану
хотя и принадлежит булеану 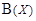 , но не имеет прообраза
, но не имеет прообраза 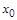 во множестве X.
во множестве X.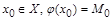 . Тогда возможны два варианта: а)
. Тогда возможны два варианта: а) 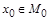 , б)
, б) 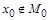 .
.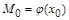 и
и 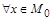 выполняется
выполняется 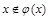 , следовательно,
, следовательно, 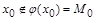 . Аналогично невозможен и случай б):
. Аналогично невозможен и случай б): 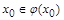 , но
, но 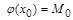 . Полученное противоречие показывает, что не существует элемента
. Полученное противоречие показывает, что не существует элемента 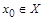 , являющегося прообразом множества
, являющегося прообразом множества 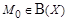 .
.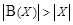 .
.


