Рассмотрим множество  R. Сравним его с множеством N. Очевидно, что
R. Сравним его с множеством N. Очевидно, что  ½ N ½. Действительно, отрезок [0; 1] содержит счетное подмножество
½ N ½. Действительно, отрезок [0; 1] содержит счетное подмножество 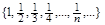 , значит, является не менее, чем счетным. Покажем, что [0; 1] и N не являются равномощными множествами, т.е. что
, значит, является не менее, чем счетным. Покажем, что [0; 1] и N не являются равномощными множествами, т.е. что  .
.
Теорема. Множество точек отрезка [0; 1] не является счетным.
Проведем доказательство методом “от противного”. Предположим, что множество [0; 1] счетно, т.е. существует биекция N на [0; 1], и каждому элементу отрезка можно присвоить номер:  N }. Каждый элемент отрезка [0; 1] представляется в виде бесконечной десятичной дроби
N }. Каждый элемент отрезка [0; 1] представляется в виде бесконечной десятичной дроби  , где
, где 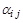 – j -я десятичная цифра i -го элемента. Запишем все элементы
– j -я десятичная цифра i -го элемента. Запишем все элементы  N, в порядке возрастания номеров. Покажем, что найдется элемент b, принадлежащий отрезку [0; 1], но не совпадающий ни с одним из занумерованных элементов
N, в порядке возрастания номеров. Покажем, что найдется элемент b, принадлежащий отрезку [0; 1], но не совпадающий ни с одним из занумерованных элементов  N. Метод построения такого элемента называется диагональной процедурой Кантора и заключается в следующем. Будем строить элемент b в виде бесконечной десятичной дроби
N. Метод построения такого элемента называется диагональной процедурой Кантора и заключается в следующем. Будем строить элемент b в виде бесконечной десятичной дроби  , где
, где  – i -я десятичная цифра. В качестве
– i -я десятичная цифра. В качестве 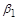 возьмем любую цифру, не совпадающую с
возьмем любую цифру, не совпадающую с  ,
,  – любую цифру, не совпадающую с
– любую цифру, не совпадающую с  , и т.д.,
, и т.д.,  при любых
при любых  N (рис. 1.26). Построенный таким образом элемент b принадлежит отрезку[0; 1], но отличается от каждого из занумерованных элементов
N (рис. 1.26). Построенный таким образом элемент b принадлежит отрезку[0; 1], но отличается от каждого из занумерованных элементов  хотя бы одной цифрой. Следовательно, предположение о том, что существует биекция
хотя бы одной цифрой. Следовательно, предположение о том, что существует биекция 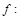 N ® [0; 1]ошибочно, и множество [0; 1] не является счетным.
N ® [0; 1]ошибочно, и множество [0; 1] не является счетным.

Рис. 1.26. Диагональная процедура Кантора
Итак, мы показали, что ½ [0; 1]½ > ½ N ½, т.е. класс эквивалентности, которому принадлежит отрезок [0; 1], расположен правее класса À 0 счетных множеств в ряду мощностей (рис. 1.25). Обозначим этот класс À (без индекса). Множества, принадлежащие этому классу, называются несчетными или множествами мощности континуум (континуум – непрерывный). Этому классу принадлежат и интервал (0; 1), и множество R действительных чисел, и множество точек круга на плоскости.
Пример. Множество R имеет мощность континуума, т.к. равномощно отрезку [0; 1]. Действительно, по теореме Кантора-Бернштейна (см. 1.4.3) ½ [0; 1]½ = ½ (0; 1)½. Биекцию интервала (0; 1)на множество R можно задать с помощью сложной функции  , где
, где  имеет вид
имеет вид  и отображает интервал (0; 1)на интервал
и отображает интервал (0; 1)на интервал  , а
, а  отображает интервал
отображает интервал  на R по закону
на R по закону 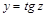 .
.

 R. Сравним его с множеством N. Очевидно, что
R. Сравним его с множеством N. Очевидно, что  ½ N ½. Действительно, отрезок [0; 1] содержит счетное подмножество
½ N ½. Действительно, отрезок [0; 1] содержит счетное подмножество 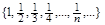 , значит, является не менее, чем счетным. Покажем, что [0; 1] и N не являются равномощными множествами, т.е. что
, значит, является не менее, чем счетным. Покажем, что [0; 1] и N не являются равномощными множествами, т.е. что  .
. N }. Каждый элемент отрезка [0; 1] представляется в виде бесконечной десятичной дроби
N }. Каждый элемент отрезка [0; 1] представляется в виде бесконечной десятичной дроби  , где
, где 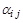 – j -я десятичная цифра i -го элемента. Запишем все элементы
– j -я десятичная цифра i -го элемента. Запишем все элементы  N, в порядке возрастания номеров. Покажем, что найдется элемент b, принадлежащий отрезку [0; 1], но не совпадающий ни с одним из занумерованных элементов
N, в порядке возрастания номеров. Покажем, что найдется элемент b, принадлежащий отрезку [0; 1], но не совпадающий ни с одним из занумерованных элементов  , где
, где  – i -я десятичная цифра. В качестве
– i -я десятичная цифра. В качестве 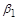 возьмем любую цифру, не совпадающую с
возьмем любую цифру, не совпадающую с  ,
,  – любую цифру, не совпадающую с
– любую цифру, не совпадающую с  , и т.д.,
, и т.д.,  при любых
при любых  N (рис. 1.26). Построенный таким образом элемент b принадлежит отрезку[0; 1], но отличается от каждого из занумерованных элементов
N (рис. 1.26). Построенный таким образом элемент b принадлежит отрезку[0; 1], но отличается от каждого из занумерованных элементов  хотя бы одной цифрой. Следовательно, предположение о том, что существует биекция
хотя бы одной цифрой. Следовательно, предположение о том, что существует биекция 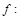 N ® [0; 1]ошибочно, и множество [0; 1] не является счетным.
N ® [0; 1]ошибочно, и множество [0; 1] не является счетным.

 , где
, где  имеет вид
имеет вид  и отображает интервал (0; 1)на интервал
и отображает интервал (0; 1)на интервал  , а
, а  отображает интервал
отображает интервал 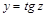 .
.


