Классы равномощных множеств
Введенное в 1.4.1 отношение равномощности является отношением эквивалентности “ º “. В самом деле, оно рефлексивно: для каждого множества Х справедливо По свойству отношения эквивалентности (см. 1.2.5) получаем разбиение всех множеств на непересекающиеся классы равномощных множеств. Каждому классу присвоим название - кардинальное число. Таким образом, кардинальное число – это то общее, что есть у всех равномощных множеств. Обозначим кардинальное число множества
1.4.3. Сравнение множеств по мощности
Расположим классы эквивалентности равномощных множеств в порядке возрастания кардинальных чисел: Для конечных множеств это не вызывает затруднений: 1) если множества X и Y попадают в один класс эквивалентности, пишем ½ X ½ =½ Y ½; 2) если класс эквивалентности множества X находится левее класса эквивалентности Y в ряду кардинальных чисел, используем обозначение ½ X ½ < ½ Y ½; 3) если класс эквивалентности множества X находится правее класса эквивалентности множества Y, то ½ X ½ > ½ Y ½; 4) в теории множеств строго доказано, что случай, когда множества X и Y несравнимы по мощности, невозможен – это означает, что классы равномощных множеств можно вытянуть в цепочку без разветвлений по возрастанию мощности. Следующая теорема, приведенная без доказательства, позволяет устанавливать равномощность бесконечных множеств. Теорема Кантора-Бернштейна. Пусть X и Y два бесконечных множества. Если во множестве X есть подмножество, равномощное множеству Y, а во множестве Y есть подмножество, равномощное X, то множества X и Y равномощны. Пример. Пусть
В качестве подмножества
|

 (Х равномощно Х), так как существует тождественное отображение множества Х на множество Х. Это отношение симметрично: если существует биекция X на Y, то обратное отображение также является биекцией (если
(Х равномощно Х), так как существует тождественное отображение множества Х на множество Х. Это отношение симметрично: если существует биекция X на Y, то обратное отображение также является биекцией (если  , то
, то  ). Отношение транзитивно: если существует биекция
). Отношение транзитивно: если существует биекция  и существует биекция
и существует биекция  , то соответствие
, то соответствие  отображает X на Z биективно (если
отображает X на Z биективно (если 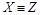 ).
). или ½ Х ½. Пустое множество имеет кардинальное число
или ½ Х ½. Пустое множество имеет кардинальное число  Æ =0; для всех конечных множеств кардинальное число совпадает с количеством элементов множества; а для обозначения кардинального числа бесконечных множеств используется буква À (алеф). Понятие кардинального числа (мощности множества) обобщает понятие “ количество элементов ” на бесконечные множества.
Æ =0; для всех конечных множеств кардинальное число совпадает с количеством элементов множества; а для обозначения кардинального числа бесконечных множеств используется буква À (алеф). Понятие кардинального числа (мощности множества) обобщает понятие “ количество элементов ” на бесконечные множества. .
. означает для конечных множеств, что количество элементов множества X меньше количества элементов множества Y, и класс ½ X ½ расположен левее класса ½ Y ½ в последовательности классов равномощных множеств. А что означает неравенство ½ X ½ < ½ Y ½ для бесконечных множеств? Договоримся о следующих обозначениях:
означает для конечных множеств, что количество элементов множества X меньше количества элементов множества Y, и класс ½ X ½ расположен левее класса ½ Y ½ в последовательности классов равномощных множеств. А что означает неравенство ½ X ½ < ½ Y ½ для бесконечных множеств? Договоримся о следующих обозначениях: . Покажем, что ½ X ½ =½ Y ½. Непосредственно биекцию X на Y построить трудно, т.к. X - отрезок с включенными концами, а Y – открытый интервал.
. Покажем, что ½ X ½ =½ Y ½. Непосредственно биекцию X на Y построить трудно, т.к. X - отрезок с включенными концами, а Y – открытый интервал.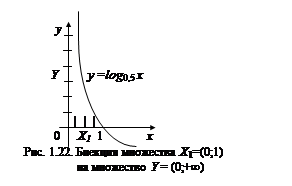 Применим теорему Кантора-Бернштейна. Возьмем в качестве подмножества
Применим теорему Кантора-Бернштейна. Возьмем в качестве подмножества  множества X открытый интервал:
множества X открытый интервал:  . Биекция
. Биекция  (рис. 1.22), осуществляется взаимно однозначное отображение интервала (0; 1) на интервал
(рис. 1.22), осуществляется взаимно однозначное отображение интервала (0; 1) на интервал  .
. возьмем любой замкнутый интервал из Y, например,
возьмем любой замкнутый интервал из Y, например, 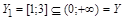 . В 1.4.1 уже показано, что ½ [1; 3]½ =½ [0; 1]½ (существует биекция
. В 1.4.1 уже показано, что ½ [1; 3]½ =½ [0; 1]½ (существует биекция 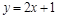 ). Таким образом, условия теоремы Кантора-Бернштейна выполняются, следовательно, множества
). Таким образом, условия теоремы Кантора-Бернштейна выполняются, следовательно, множества  и
и  равномощны (½ X ½ =½ Y ½).
равномощны (½ X ½ =½ Y ½).


