Определение счетного множества
Будем говорить, что множество X счетно, если оно равномощно множеству натуральных чисел N. Пример 1. Пусть X множество нечетных натуральных чисел. Покажем, что X счетно. Для этого нужно установить биекцию множества X на множество натуральных чисел, т.е. занумеровать элементы множества X так, чтобы каждому элементу X соответствовал ровно один номер, а любому натуральному числу соответствовал ровно один элемент из X. Очевидно, соответствие
Таким образом, ½ X ½ =½ N ½ и X счетно. Пример 2. Пусть X= N´ N – декартово произведение множества N на себя. Покажем, что X счетно. Расположим все элементы X в виде матрицы (рис. 1.24) и занумеруем его элементы “ по диагоналям ”: номер 1 присвоим элементу (1, 1), номер 2 – элементу (2, 1), 3 – (1, 3) и т.д.
Полученное отображение X на N также является биекцией (хотя записать формулу в явном виде сложнее, чем в примере 1). Мощность счетного множества обозначается À 0. Когда мы пишем ½ X ½ =À 0, мы утверждаем, что множество X счетно, т.е. относится к тому же классу эквивалентности, что и множество натуральных чисел. А множество N считается эталоном (образцом) счетных множеств.
|
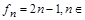N, удовлетворяет этим требованиям:
