Свойства конечных множеств
Множество X называется конечным, если существует биекция Все множества, для которых такую биекцию установить невозможно, будем называть бесконечными. Пустое множество принято относить к конечным множествам и обозначать ½ Æ ½ =0. Сформулируем свойства конечных множеств в виде теорем (не все теоремы будут строго доказаны). Теорема (правило суммы). Пусть множество X является объединением r непересекающихся конечных множеств Согласно условию теоремы система множеств Шаг 1. Покажем, что теорема справедлива при
является биекцией Шаг 2. Индукционный переход заключается в следующем: предположим, что теорема справедлива при числе блоков разбиения Предположение: множества Рассмотрим разбиение множества X на r конечных множеств. Тогда Заключение. Согласно методу математической индукции, теорема справедлива для любого натурального числа r блоков разбиения. Теорема (правило произведения). Пусть конечное множество X представлено в виде декартова произведения r конечных множеств Правило произведения доказывается методом математической индукции аналогично правилу суммы. Теорема (о мощности булеана конечного множества). Пусть множество X конечно и Напомним, что B (X) есть булеан множества X, т.е. множество всех подмножеств множества X. При построении булеана в 1.1.8 мы использовали эту теорему без доказательства. Доказательство. Множество X конечно, значит, существует биекция
Установим взаимно однозначное соответствие (биекцию) Теорема (правило включения – исключения). Пусть Доказательство теоремы опирается на правило суммы. Представим множество
Теорема (обобщенное правило включения – исключения). Пусть конечное множество X является объединением r конечных множеств:
Теорема доказывается методом математической индукции по числу r блоков покрытия множества X.
|

 , т.е. множество X можно взаимно однозначно отобразить на отрезок натурального ряда {1, 2, …, n }; при этом ½ X ½ = n.
, т.е. множество X можно взаимно однозначно отобразить на отрезок натурального ряда {1, 2, …, n }; при этом ½ X ½ = n. . Тогда
. Тогда  .
. является разбиением множества X. Доказательство проведем методом математической индукции по числу r блоков разбиения.
является разбиением множества X. Доказательство проведем методом математической индукции по числу r блоков разбиения. . Пусть
. Пусть  Æ и множества
Æ и множества  конечны, т.е. существует биекция
конечны, т.е. существует биекция  и
и  . Установим биекцию
. Установим биекцию  следующим образом: всем элементам множества
следующим образом: всем элементам множества  оставим прежние номера, а номера элементов множества
оставим прежние номера, а номера элементов множества  увеличим на число
увеличим на число  . Полученное отображение
. Полученное отображение
 в силу биективности
в силу биективности  и
и  . Следовательно,
. Следовательно, 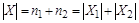 . Основание индукции доказано.
. Основание индукции доказано. ; докажем, что в этом случае она будет справедлива и при числе блоков r.
; докажем, что в этом случае она будет справедлива и при числе блоков r. , конечны и образуют разбиение множества Y. Тогда
, конечны и образуют разбиение множества Y. Тогда 
 по закону ассоциативности объединения. Обозначим
по закону ассоциативности объединения. Обозначим  Опираясь на основание индукции (шаг 1), имеем
Опираясь на основание индукции (шаг 1), имеем  , а по индукционному предположению
, а по индукционному предположению  Индукционный переход доказан.
Индукционный переход доказан. . Тогда
. Тогда  .
.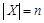 . Тогда
. Тогда  .
. . Зафиксируем порядок элементов множества
. Зафиксируем порядок элементов множества  и рассмотрим множество V всех упорядоченных наборов длины n, состоящих из нулей и единиц:
и рассмотрим множество V всех упорядоченных наборов длины n, состоящих из нулей и единиц: .
. следующим образом: элементу
следующим образом: элементу  сопоставляем множество
сопоставляем множество  , содержащее те и только те элементы
, содержащее те и только те элементы  , для которых
, для которых  . Легко проверить, что данное соответствие является биекцией. Таким образом, множество V и
. Легко проверить, что данное соответствие является биекцией. Таким образом, множество V и 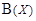 равномощны. Но множество
равномощны. Но множество  V является декартовым произведением n одинаковых сомножителей
V является декартовым произведением n одинаковых сомножителей  , т.е.
, т.е.  и по теореме о мощности произведения
и по теореме о мощности произведения  , следовательно, и
, следовательно, и  .
. .
. в виде объединения непересекающихся множеств
в виде объединения непересекающихся множеств  , где
, где  ,
, 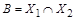 ,
, 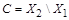 (рис. 1.23). Тогда по правилу суммы
(рис. 1.23). Тогда по правилу суммы  , но
, но  , поэтому
, поэтому  ,
,  . Имеем
. Имеем  , отсюда
, отсюда 
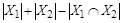 .
.
 Тогда
Тогда 



