ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
1. Сколько различных дробей можно составить из чисел 3, 5, 7, 11, 13, 17 так, чтобы в каждую дробь входили 2 различных числа? Сколько среди них будет правильных дробей? Решение. Из шести простых чисел: 3, 5, 7, 11, 13, 17 можно составить Из этих 30 дробей ровно половина, т.е. 15 штук, будут правильные ( Ответ: 30; 15. 2. По 10 воздушным целям запускается 7 ракет. Для каждой ракеты равновозможен выбор любой цели независимо от выбора целей для других ракет. Найти вероятность того, что ракеты запущены по разным целям. Решение. Применяем классическое определение вероятности Ответ: 0, 6048. 3. Путешественника с вероятностью 0, 5 может укусить слепень, с вероятностью 0, 9 – комар и с вероятностью 0, 2 – оса. Какова вероятность того, что путешественник: а) получит только один укус; б) получит хотя бы один укус? Решение. Пусть а) Событие A, означающее, что путешественник получит только один укус, записывается в виде:
Так как
б) Событие B, означающее, что путешественник получит хотя бы один укус, записывается в виде
Так как укусы насекомых – независимые в совокупности события, то Ответ: 0, 41; 0, 91. 4. Вероятность безотказной работы каждого элемента в течение времени Т равна р. Элементы работают независимо и включены в цепь по приведённой схеме. Пусть событие
Решение. а) Цепь состоит из двух последовательно включённых блоков. Цепь работает, когда два блока работают совместно. Присвоим блокам номера I, II слева направо. Пусть б) Так как элементы, а, следовательно, и блоки работают независимо, то можно применить теоремы сложения и умножения вероятностей для взаимно независимых событий. Вероятность события Ответ: а) 5. В детском наборе «Кубики» имеется четыре белых, три красных и пять синих кубиков. Один кубик из набора потеряли. Если из оставшегося набора наугад выбрать кубик, то какова вероятность того, что он будет белым? Если выбранный кубик оказался белым, то какова вероятность того, что был утерян синий кубик? Решение. Пусть событие Введем следующие гипотезы:
Из условий задачи находим вероятности:
По формуле полной вероятности находим:
С помощью формулы Байеса получаем ответ на второй вопрос задачи:
Ответ: 6. Среди волков встречаются оборотни, доля которых составляет 10%. Какова вероятность, что среди пяти волков окажется не более двух оборотней? Решение. Для решения задачи используем схему Бернулли. Здесь число наблюдений n=5. Пусть X – число оборотней среди пяти волков. Тогда по формуле Бернулли получаем:
где p – вероятность того, что произвольно выбранный волк окажется оборотнем. По условию задачи р =0, 1. Таким образом, искомая вероятность равна:
Ответ: 0, 99144. 7. Аппарат состоит из 2000 элементов. Вероятность отказа одного элемента в течение года равна 0, 001. Какова вероятность отказа двух элементов за год? Какова вероятность отказа не менее двух элементов за год? Решение. Для решения задачи используем приближённую формулу в схеме Бернулли – формулу Пуассона. Работу каждого элемента рассматриваем как отдельное испытание. Введём событие A – отказ элемента за год. Имеем: По формуле Пуассона: Найдём вероятность события B – отказа не менее двух элементов за год: Ответ: 0, 2707; 0, 594. 8. В урне 5 белых и 4 чёрных шара. Из неё последовательно вынимают шары до первого появления белого шара. Построить ряд распределения дискретной случайной величины X – числа извлечённых шаров. Решение. Возможными значениями с.в. X являются числа
(Контроль: Таким образом, ряд распределения д.с.в. X имеет вид:
9. Дискретная случайная величина X задана своим законом распределения.
а) Заполнить пустую клетку таблицы и найти математическое ожидание, дисперсию и среднее квадратическое отклонение данной случайной величины. Построить график её функции распределения. б) Найти закон распределения и математическое ожидание случайной величины Решение. а) Так как Таким образом, закон распределения с.в. X имеет вид:
Найдём математическое ожидание с.в. X, используя формулу
Найдём дисперсию с.в. X, используя формулу Закон распределения с.в.
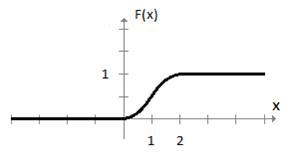
Тогда Найдём функцию распределения По определению функции распределения получаем: если если если если
если
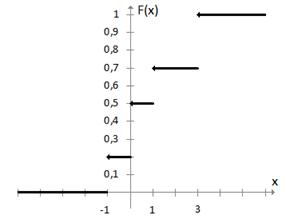
График функции
б) Найдём закон распределения и математическое ожидание случайной величины Возможные значения с.в. Y таковы:
Найдём M [ Y ]: Ответ: а) б)
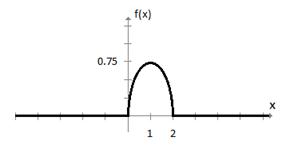
10. Дана плотность вероятности
Найти: а) значение параметра C; б) функцию распределения вероятности в) математическое ожидание г) д) построить графики Решение. а) Найдём значение параметра С, исходя из того, что
Таким образом:
б) Найдём
в) Найдём математическое ожидание
г) Найдём
д) построим графики
11. Определить закон распределения случайной величины X, если её плотность вероятности имеет вид:
Найти: а) б) среднее квадратическое отклонение в) значение коэффициента А; г) д) Решение. Сравнив данную функцию
с плотностью а) Очевидно, что б) в) Значение коэффициента А найдём из равенства
г) д)
Значение 12. Задана таблица распределения дискретной двумерной случайной величины.
Найти: а) значение коэффициента d; б) безусловные законы распределения случайных величин X и Y; в) математические ожидания г) дисперсии д) корреляционный момент и коэффициент корреляции системы случайных величин X и Y; е) установить, зависимы или нет компоненты X и Y. Решение. а) Значение коэффициента d найдём, используя тот факт, что б) Найдём безусловные законы распределения случайных величин X и Y; Случайная величина X принимает два значения
Следовательно, закон распределения с.в. X (т.е. безусловный закон распределения компоненты X) можно представить в виде:
Аналогично получаем безусловный закон распределения компоненты Y:
в) Найдём математические ожидания
г) Найдём дисперсии
Аналогично:
д) Найдём корреляционный момент и коэффициент корреляции системы случайных величин X и Y; Корреляционный момент
Находим коэффициент корреляции:
е) Установим, зависимы или нет компоненты X и Y. Так как 13. Дана плотность вероятности
Найти: а) значение коэффициента C; б) безусловные законы распределения случайных величин X и Y; в) математические ожидания г) дисперсии д) корреляционный момент и коэффициент корреляции системы случайных величин X и Y; е) установить, зависимы или нет компоненты X и Y. а) Коэффициент С находим из условия
Отсюда б) Найдём безусловные законы распределения с.в. X и Y;
Так как переменные x и y входят в функцию в) Найдём математические ожидания Так как переменные x и y входят в функцию г) Найдём дисперсии Так как переменные x и y входят в функцию
д) Найдём корреляционный момент Предварительно найдём
е) Установим, зависимы или нет компоненты X и Y. Так как
|

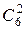
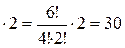 штук различных дробей (
штук различных дробей (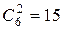 способами выбираем два числа из шести, и единственным образом составляем дробь так, чтобы числитель был меньше знаменателя).
способами выбираем два числа из шести, и единственным образом составляем дробь так, чтобы числитель был меньше знаменателя).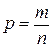 . Здесь
. Здесь  , так как каждое размещение ракет по целям есть 7- элементное соединение, в котором для каждой ракеты выбирается любая из 10 целей.
, так как каждое размещение ракет по целям есть 7- элементное соединение, в котором для каждой ракеты выбирается любая из 10 целей. 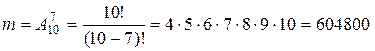 , так как если ракеты распределяются по разным целям, то для первой ракеты возможен выбор любой из 10 целей, для второй ракеты возможен выбор любой из 9 оставшихся целей и т.д. Тогда
, так как если ракеты распределяются по разным целям, то для первой ракеты возможен выбор любой из 10 целей, для второй ракеты возможен выбор любой из 9 оставшихся целей и т.д. Тогда 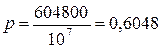 .
. – события, означающие укус путешественника слепнем, комаром и осой соответственно. Тогда
– события, означающие укус путешественника слепнем, комаром и осой соответственно. Тогда  ,
, 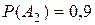 ,
, 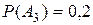 .
.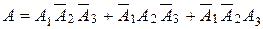 .
.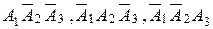 – несовместные события (насекомые кусают путешественника независимо друг от друга), то из теорем сложения и умножения вероятностей следует:
– несовместные события (насекомые кусают путешественника независимо друг от друга), то из теорем сложения и умножения вероятностей следует: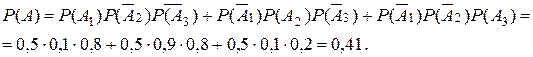
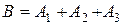 .
.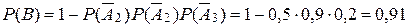 .
.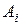 означает безотказную работу за время Т элемента с номером i (i = 1, 2, 3, …), а событие B – безотказную работу цепи. Требуется: а) написать формулу, выражающую событие B через события
означает безотказную работу за время Т элемента с номером i (i = 1, 2, 3, …), а событие B – безотказную работу цепи. Требуется: а) написать формулу, выражающую событие B через события 
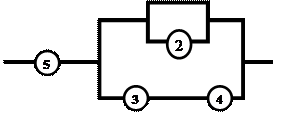
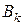 - событие, означающее безотказную работу блока с номером k (k= I, II).Событие B – безотказная работа цепи за время Т, выражается через события
- событие, означающее безотказную работу блока с номером k (k= I, II).Событие B – безотказная работа цепи за время Т, выражается через события 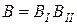 . Первый блок состоит из одного элемента с номером 5, поэтому
. Первый блок состоит из одного элемента с номером 5, поэтому 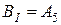 . Второй блок состоит из четырёх элементов два из которых (3 и 4) включены последовательно и два (1 и 2) включены параллельно. Поэтому блок работает, когда работает хотя бы один из элементов 1 и 2, или работают элементы 3 и 4 одновременно, либо то и другое вместе, следовательно,
. Второй блок состоит из четырёх элементов два из которых (3 и 4) включены последовательно и два (1 и 2) включены параллельно. Поэтому блок работает, когда работает хотя бы один из элементов 1 и 2, или работают элементы 3 и 4 одновременно, либо то и другое вместе, следовательно, 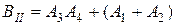 . Таким образом,
. Таким образом, 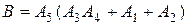 .
.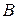 будет равна:
будет равна: 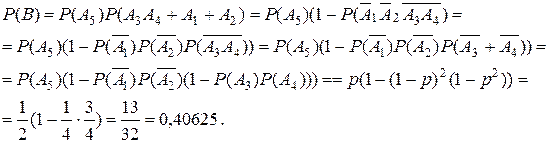
 – выбранный кубик – белый.
– выбранный кубик – белый.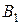 – был утерян белый кубик;
– был утерян белый кубик;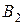 – был утерян красный кубик;
– был утерян красный кубик;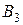 – был утерян синий кубик.
– был утерян синий кубик. ;
;  ;
; 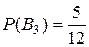 ;
;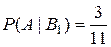 ;
; 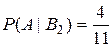 ;
;  .
.
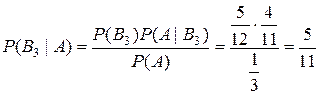 .
.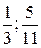 .
.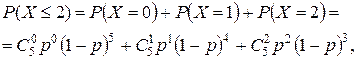
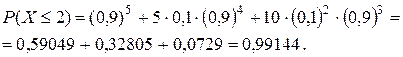
 .
.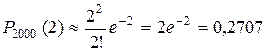 .
.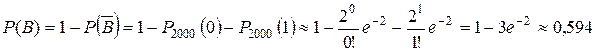 .
.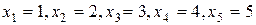 . Соответствующие им вероятности
. Соответствующие им вероятности 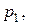
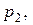
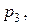

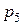 найдем, воспользовавшись правилом умножения вероятностей.
найдем, воспользовавшись правилом умножения вероятностей.
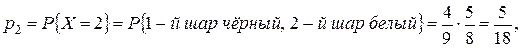

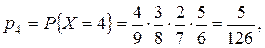
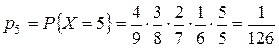 .
.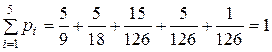 .)
.)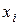
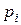
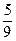
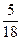
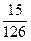
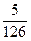
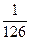
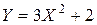 .
.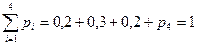 , то
, то 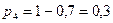 .
.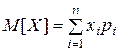 :
: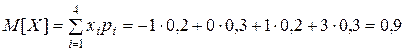 .
. .
.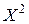 запишем в виде таблицы распределения:
запишем в виде таблицы распределения: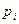
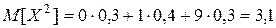 ;
; 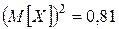 . Следовательно,
. Следовательно, 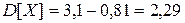 . Среднее квадратическое отклонение случайной величины X равно
. Среднее квадратическое отклонение случайной величины X равно 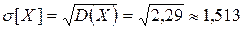 .
.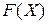 и построим её график.
и построим её график.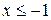 , то
, то  ;
;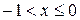 , то
, то 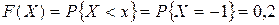 ;
;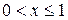 , то
, то 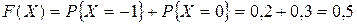 ;
;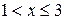 , то
, то 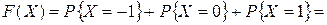
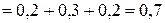 ;
;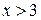 , то
, то 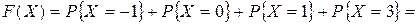
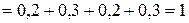 .
. Таким образом,
Таким образом, 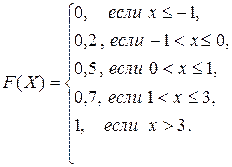
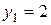 ,
, 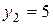 ,
, 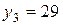 . Вероятности этих значений равны вероятностям соответствующих значений с.в.
. Вероятности этих значений равны вероятностям соответствующих значений с.в. 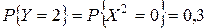 и т.д.). Таким образом:
и т.д.). Таким образом: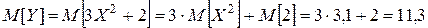 .
. ;
; 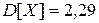 ;
; 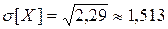 ;
;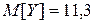 .
.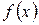 случайной величины X.
случайной величины X.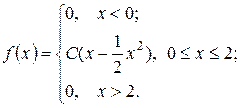
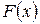 ;
; , дисперсию и среднее квадратическое отклонение данной случайной величины;
, дисперсию и среднее квадратическое отклонение данной случайной величины;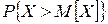 ;
;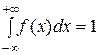 .
.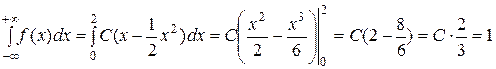 , а значит,
, а значит,  .
.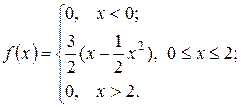
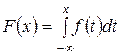 .
.
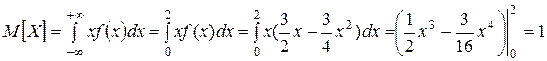 ,
,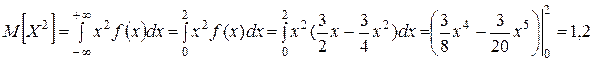 , тогда
, тогда 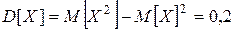 и
и 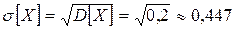 .
.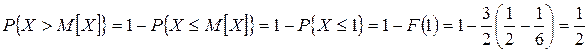 .
.
 .
.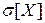 ;
;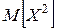 ;
; .
.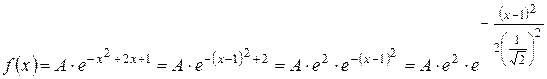
 нормального распределения, приходим к выводу, что с.в. X имеет нормальное распределение.
нормального распределения, приходим к выводу, что с.в. X имеет нормальное распределение.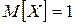 .
.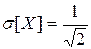 .
.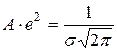 , где
, где  . Отсюда
. Отсюда 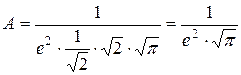 . Следовательно, плотность вероятности с.в. X имеет вид:
. Следовательно, плотность вероятности с.в. X имеет вид: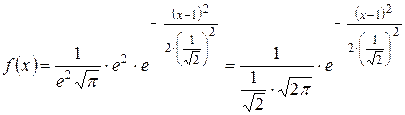 .
.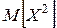 найдём, используя формулу
найдём, используя формулу  .
.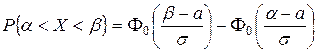 .
.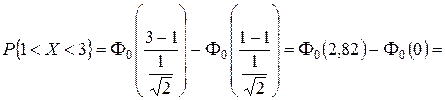
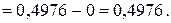
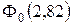 найдено по таблице значений функции
найдено по таблице значений функции 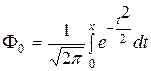 .
.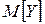 ;
;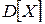 и
и  , среднеквадратические отклонения
, среднеквадратические отклонения 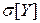 ;
;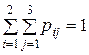 . Коэффициент
. Коэффициент 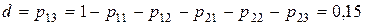 .
.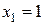 и
и 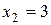 . Вероятности этих значений соответственно равны:
. Вероятности этих значений соответственно равны: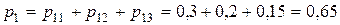 ,
, 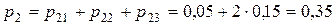 .
.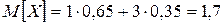 ;
; 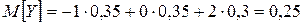 .
.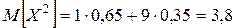 ;
;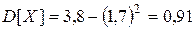 .
. ;
; 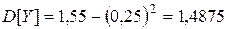 ;
;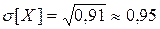 ;
; 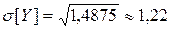 .
.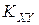 найдем, используя формулу:
найдем, используя формулу: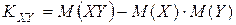 :
: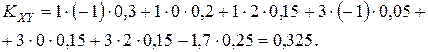
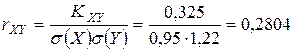 .
.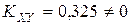 , то с.в. X и Y зависимы, т.е. с.в. являются коррелированными.
, то с.в. X и Y зависимы, т.е. с.в. являются коррелированными.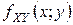 двумерной случайной величины:
двумерной случайной величины: где
где 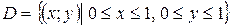 .
.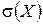 ,
, 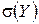 ;
;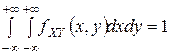 .
.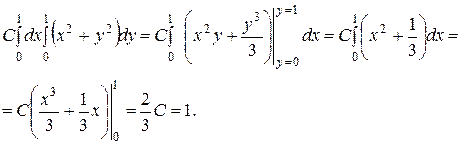
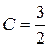 .
.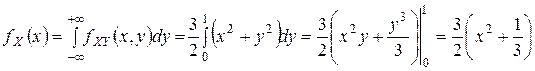 при
при 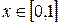 ;
; 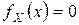 при
при  .
.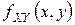 равноправно, то
равноправно, то  при
при 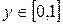 ;
; 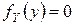 при
при 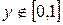 .
.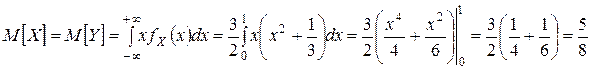 .
.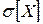 ,
, 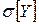 ;
; 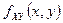 равноправно, то
равноправно, то 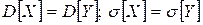 .
.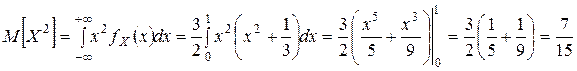 ;
; ;
;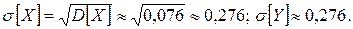
 системы случайных величин X и Y;
системы случайных величин X и Y; .
.
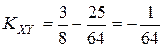 ;
;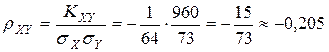 .
.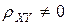 , то X, Y зависимы.
, то X, Y зависимы.


