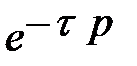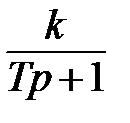Определение. Классификация типовых звеньев

В ТАУ при моделировании систем применяют так называемые типовые звенья, которые приближенно соответствуют элементам реальных систем. Основных типовых звеньев всего шесть. В связи с этим, построение моделей САУ довольно простой процесс. Самое сложное – это анализ характеристик системы и изменение (подбор, корректировка) характеристик управляющего устройства с целью улучшения качества процесса управления (регулирования).

Типовые звенья упрощают структурное моделирование системы управления.

Функциональное назначение элементов системы не зависит от физической природы управляемой величины, ни от физической природы аппаратуры, из которой построена система управления. Величина y(t) может быть напряжением, положением осей в следящем приводе или температурой в электропечи.

С этой точки зрения все элементы (звенья) системы можно разбить по характеру процессов протекающих в них на:

- пропорциональное (усилительное) звено;

- интегрирующее звено;

- апериодическое звено (инерционное звено первого порядка);

- колебательное звено (инерционное звено второго порядка);

- дифференцирующее звено;

- запаздывающее звено;

Тип звена однозначно определяется законом, связывающим между собой величины х(t) и y(t).

 

8.5.2. Пропорциональное звено.

 

Пропорциональное звено это такое звено, выходной сигнал y(t) которого пропорционален входному x(t):

y = k· x.

Поэтому, передаточная функция пропорционального звена равна

 

W(p) = k.

Таким образом, пропорциональное звено является без инерционным.

 

К

x y

 

 

Рис. 40. Структурная схема пропорционального звена

 

Замечание: в статическом режиме многие отдельные звенья и даже целые системы автоматического управления (САУ) можно промоделировать пропорциональным звеном.

Это звено выполняет следующее преобразование – входной сигнал умножается на постоянную величину k, которая называется коэффициентом усиления или коэффициентов передачи. Этот коэффициент может быть размерным, он может иметь любое действительное значение, как положительное, так и отрицательное.

График переходной функции усилительного звена приведен на рисунке.

h

к h(t)

1 1(t) t

Рис. 41. Переходная функция пропорционального звена

 

Рассмотрим некоторые примеры пропорциональных звеньев. На рисунке 42.а схематически изображен усилитель постоянного тока. Пусть его входное напряжение u₁, а выходное u₂. Величины входного и выходного напряжения связаны между собой зависимостью u₂=k u₁. Безразмерная постоянная величина kесть коэффициент усиления звена.

k

∆ X₂

u₁ u₂ u₂ R А 0 В

I ∆ x₁

а) в) с)

Рис. 42. Примеры пропорциональных звеньев

 

На рисунке 42.в изображено сопротивление R, на зажимы которого подано напряжение U. Ток в цепи сопротивления I равен U/R. Если считать напряжение входной величиной, а ток – входной, то это звено является пропорциональным. На рисунке 42.с изображен рычаг. Пусть вертикальная составляющая перемещения его левого конца Δ X₁ есть входная величина, вертикальная составляющая перемещения правого конца Δ X ₂- выходная величина. Тогда Δ X ₂= k Δ X ₁ и данное звено является пропорциональным. Величина k больше или меньше единицы в зависимости от соотношения плеч рычага. Пропорциональными звеньями моделируются усилители, редукторы, делители напряжения и т.п.

8.5.3. Интегрирующее звено. Интегрирующим звеном называется такое, выходной сигнал которого пропорционален интегралу по времени от входного сигнала:

где Т – постоянная времени интегратора, сек.

Как видно, интегратор накапливает входной сигнал с течением времени. Постоянная времени интегратора T численно характеризует скорость этого накопления. Структурная схема выгляди следующим образом.

 

х (t) y(t)

 

Рис. 43. Структурная схема интегрирующего звена

Передаточная функция интегратора:

W(p) = k/ p.

где k = 1/Т – коэффициент усиления интегратора.

Реакция интегрирующего звена на входной сигнал 1(t) имеет вид (пер. функ.):

h(t) = k ⋅ t при t ≥ 0. Таким образом, переходная функция интегрирующего звена имеет вид наклонной прямой, исходящей из нуля под углом α;, причем k = tg α.

h h(t)

1 1(t)

α

0 T t

Рис. 44. Переходная функция интегрирующего звена

 

Переходная функция интегратора линейно растет с течением времени. Скорость роста обратно пропорциональна постоянной времени интегратора. Выходной сигнал интегратора достигает уровня ступенчатой функции за время, равное постоянной времени Т интегратора. Это позволяет определять постоянную времени интегратора по его экспериментально снятой характеристике.

Примером интегрирующего звена может служить емкость, наполняющаяся жидкостью, емкости (электрическая и гидравлическая), вал двигателя, угол поворота которого пропорционален интегралу от частоты вращения и др.

 

 

V   h

Рис.45. Примеры интегрирующих звеньев

 

Интегрирующее звено не может находиться в состоянии равновесия при любом постоянном значении входного сигнала. При любом сколь мало отличном от нуля постоянном входном сигнале выходной сигнал может стать через достаточно большое время сколь угодно большим.

 

8.5.4. Дифференцирующее звено. Дифференцирующим звеном называется такое, выходной сигнал которого пропорционален производной по времени от входного сигнала: y(t) = k ⋅ dx(t) /dt, то есть скорости изменения входной величины с коэффициентом передачи k.

Структурная схема выгляди следующим образом.

х (t) y(t)

Рис. 46. Структурная схема интегрирующего звена

 

Передаточная функция этого звена равна:

W(p) = k ∙ p.

Переходная функция дифференцирующего звена h(t) есть производная от единичной функции 1(t). Производной от единичной функции является δ (t) -функция, то есть:

d1(t)/ d t = δ.

График переходной функции дифференцирующего звена представлен на рисунке 48.

Уравнение переходной функции совпадает с уравнением δ (t) - функции и может быть записано как:

h(t) = { 0, t≠ 0

∞, t=0

h(t)

 

t

Рис. 47. Переходная функция интегрирующего звена

 

Различают идеальное и реальное дифференцирующие звенья. Идеальное дифференцирующее звено реализовать невозможно, так как величина всплеска выходной величины при подаче на вход единичного ступенчатого воздействия всегда ограничена. На практике используют реальные дифференцирующие звенья, осуществляющие приближенное дифференцирование входного сигнала.

Его уравнение: y(Tp + 1) = kpx. При малых Т звено можно рассматривать как идеальное дифференцирующее.

W(p) = k ∙ p.

 

 

При подаче на вход единичного ступенчатого воздействия выходная величина оказывается ограничена по величине и растянута во времени. По переходной характеристике, имеющей вид экспоненты, можно определить передаточный коэффициент k и постоянную времени Т.

Переходная функция реального дифференцирующего звена имеет в точке t = 0 равна h(0)=k; при t → ∞ функция h (t) → 0.

h(t)

k

1(t)

t

T

Рис. 48. Переходная функция реального дифференцирующего звена

Примерами таких звеньев могут являться четырехполюсник из сопротивления и емкости или сопротивления и индуктивности. Дифференцирующие звенья являются главным средством, применяемым для улучшения динамических свойств САУ.

 

 

Рис. 49. Примеры дифференцирующих звеньев

8.5.5. Звено запаздывания. Звено запаздывания задерживает выходной сигнал по времени относительно входного на время τ.

Уравнение звена запаздывания описывается следующим соотношением:

y(t) = x(t − τ), τ > 0.

Структурная схема выгляди следующим образом.

х (t) y(t)

 

Рис. 50. Обозначение звена запаздывания на структурной схеме

 

Это значит, что звено запаздывания выполняет «сдвиг» входного сигнала на время τ. Передаточная функция звена запаздывания:

W(p) = e ^{- p τ} , или y(t)=x(t- τ)

Переходная функция звена запаздывания h(t) = 1(t − τ). График функции приведен на рисунке 51.

h(t)

t

τ

Рис. 51. Переходная функция звена запаздывания

 

Примером звена запаздывания может служить транспортный конвейер, где входное воздействие x (t) – поток материала поступающий на конвейер, выходная переменная y(t)– поток материала уходящий с конвейера. Запаздывание определяется как:

τ = L / v,

где L– расстояние между местом подачи материала на конвейер и местом его сброса с

конвейера; v- скорость конвейера, уравнение связывающее y (t) и x (t):

y(t) = x (t –τ).

L

x

V

LL y

 

Рис. 52. Транспортный конвейер

8.5.6. Апериодическое звено (инерционное звено первого порядка).

Апериодическое это такое звено, которое описывается дифференциальным уравнением:

Tdy(t)/dt + y(t) = kx(t)

где: k – коэффициент усиления. Т – постоянная времени апериодического звена, сек.

Структурная схема выгляди следующим образом.

 

х (t) y(t)

 

Рис.53. Представление апериодического звена на структурных схемах.

Передаточная функция апериодического звена равна:

W(p) = k/ (Tp + 1).

 

Переходная характеристика апериодического звена представлен на рисунке 54. Такой процесс называется монотонным, он близок к апериодическому.

h(t)

К

1 t

0 T 3Т

Рис. 54. Переходная функция апериодического звена

 

Коэффициент усиления звена определяет уровень, к которому стремится переходная характеристика с течением времени. Касательная, проведенная в начале координат к переходной характеристике, пересекает этот уровень в момент времени, равный постоянной времени апериодического звена Т.

Апериодическое звено не сразу, а постепенно реагирует на ступенчатое воздействие, в этом и проявляется его инерционность, которая численно может характеризоваться величиной постоянной времени, поскольку переходный процесс заканчивается примерно за 3Т. За время 3Т переходная характеристика достигает 95% уровня, к которому она стремиться при стремлении времени к бесконечности.

В качестве примера апериодического звена можно привести RC – цепочку, если за входное воздействие принять напряжение u. Здесь постоянная времени T = RC, а коэффициент k = 1. Размерность постоянной времени [ RC ]=сек. Коэффициент усиления в силу одинаковой природы входного выходного сигналов безразмерен и равен в данном случае единицы. Другими примерами могут служить: термопара, электродвигатель, четырехполюсник из сопротивления и емкости или сопротивления и индуктивности.

 

 

Рис. 55. Примеры апериодических звеньев.

8.5.7. Колебательное звено (Инерционное звено второго порядка).

 

Колебательное звено это такое звено, дифференциальное уравнение которого имеет вид: T²d²y(x)/dt²+ 2 δ Tdy(t)/dt + y(t) = kx(t)

Звено характеризуется тремя параметрами:

Т – постоянная времени, сек;

k – коэффициент усиления,

δ - декремент затухания, характеризующий скорость затухания свободных колебаний звена.

Если δ < 1, звено называется колебательным.

Если δ > 1, звено называется также и инерционным звеном II порядка.

Как видно из дифференциального уравнения, передаточная функцияколебательного звена имеет вид: W(p) = k/ (T₁²p² + Т₂р+1).

х (t) y(t)

T=T₁, T₂=2 δ T

Рис. 56. Представление колебательного звена на структурной схеме

График переходной функции колебательного звена приведен на рисунке.

h(t)

 

k t

0 τ

Рис. 57. Переходная функция колебательного звена

С течением времени значения характеристик стремятся к величине коэффициентов усиления звеньев. При δ > 1 колебательность переходной функции исчезает, функция становится апериодической. Примерами колебательного звена могут служить пружина, имеющая успокоительное устройство, электрический колебательный контур. Зная характеристики реального устройства можно определить его параметры как колебательного звена. Передаточный коэффициент k равен установившемуся значению переходной функции.

Рис. 58. Пример колебательного звена.