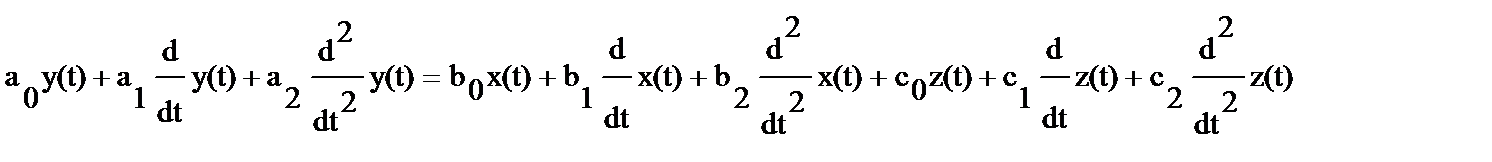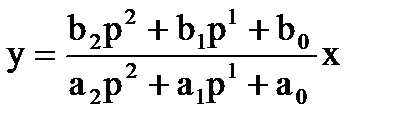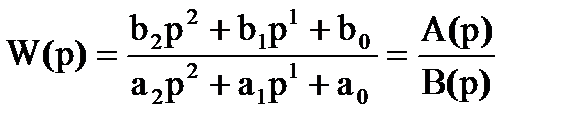Понятие передаточной функции

Каждый элемент системы автоматического управления характеризуется направленным воздействием. Он имеет вход, на который воздействует входной сигнал, изменяющийся во времени х(t). На выходе формируется выходной сигнал y(t).

 

f(x)

x(t) y(t)

z

 

В общем виде связь между входным х(t), возмущением z(t) и выходным y(t) воздействиями может быть задана в виде дифференциального уравнения.

Порядок больше 2 при описании систем не учитывается, так как это высшие гармоники. Они редко влияют на поведение системы за счет инерционности элементов системы.

Это уравнение описывает не только переходные режимы работы, но и установившиеся. Для этого достаточно положить в уравнении все производные x у и z равными нулю. Решая уравнение относительно у получим искомую статическую характеристику:

y =k_xx(t), к_x=b₀/a₀

y =k_zz(t), к_z=c₀/a₀

 

Очень важно свойство линейности. Для линейных систем (как уже отмечалось ) существует правило: реакция системы на сумму входных сигналов есть сумма реакций на каждый сигнал в отдельности. Тогда можно разделить уравнение на два – по управлению и возмущению.

В ТАУ часто используют операторную форму записи дифференциальных уравнений. При этом вводится понятие дифференциального оператора:

 

p = d/dt и p² = d²/dt²., так, что

 

dy/dt = py и d²y/dt² = p²y

Это лишь другое обозначение операции дифференцирования. Обратная дифференцированию операция интегрирования записывается как 1/p. В операторной форме исходное дифференциальное уравнение записывается как алгебраическое:

a₂p²y + a₁p¹y +a₀y = (a₂p² + a₁p¹ + a₀)y = (b₂p² + b₁p¹ + b₀)х

Уравнение динамики можно записать также в виде:

Обозначим:

 

Дифференциальный оператор W(p) называют передаточной функцией. Она определяет отношение выходной величины звена к входной в каждый момент времени: W(p) = y(t)/х(t).

Таким образом, уравнение принимает простой вид. Это есть оператор преобразования x к y, или:

y = W(p)x

А соответствующая ему схема (модель объекта) изображается следующим образом:

W(p)

x y

 

В установившемся режиме d/dt = 0, то есть p = 0, поэтому передаточная функция превращается в коэффициент передачи звена

K = b₀/a₀.

Передаточная функция является основной характеристикой звена в динамическом режиме, из которой можно получить все остальные характеристики. Она определяется только параметрами системы и не зависит от входных и выходных величин. Математическая модель САУ как раз и составляется из передаточных функций.

 

w1

w2

w3

w4

x1 x2 x3 x₄ x₅

 

x₂=w₁x₁, x₃=w₂x₂, x₄=w₃x₃, x₅=w₄x_4…

Запись соотношений между входом и выходом дает значительные преимущества при исследовании систем. В сложных системах автоматического управления имеется взаимодействие элементов: выход одного элемента служит входом другого и так далее. Использование понятия передаточной функции позволяет без труда находить связи между любыми двумя переменными.

Наличие передаточных функций элементов системы позволяет провести структурное моделирование системы управления путем замены функциональных элементов системы их математическими моделями.

Если мы будем строить математические модели различных систем, то увидим, что передаточные функции всего многообразия элементов можно свести к нескольким типовым передаточным функциям – типовым звеньям. Это в значительной мере облегчает процесс построения модели системы.

 

Мы уяснили, что такое передаточная функция. Оказывается, если мы будем строить математические модели различных систем, то увидим, что передаточные функции всего многообразия элементов можно свести к нескольким типовым передаточным функциям – типовым звеньям. Это в значительной мере облегчает процесс построения модели системы. Все типовые звенья различаются только своими динамическими характеристиками, поскольку в статике все системы суть пропорциональные звенья. Динамические характеристики типовых звеньев - это реакция их на тестовые (простейшие) сигналы.