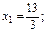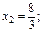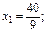Особливості методу
1. Безпосередньо з алгоритму необхідно, щоб метод гілок і границь застосовувався як для задач повністю цілочисельного програмування, так і для задач частково цілочисельного програмування. 2. Для даного методу несуттєва проблема помилок округлення. 3. Геометрична інтерпретація методу: гіперплощина, що визначається функцією мети задачі, переміщається в середину області припустимих рішень до зустрічі з найбільш близьким цілочисельним планом (див. мал.).
4. Нові обмеження виду 5. Коли вводять нові обмеження зазначеного типу, то немає необхідності розв’язувати ЗЛП заново, а можна скористатися попередньою ітерацією, уводячи нові обмеження. Розглянемо приклад. Приклад. Вирішити ЦЗЛП методом гілок і границь.
Зобразимо ОПР задачі.
Визначимо координати точки А. Для цього розв’язується система рівнянь, використовуються формули Крамера:
Таким чином, F(А) = F (13/3, 8/3) = 7. Визначимо координати точки В.
Таким чином, F(В) = F (40/9, 23/9) = 7. Процедура розгалуження здійснюється відповідно до співвідношень
Вихідна задача розпадається на дві:
|
, відіграють роль розсічень ОПР.
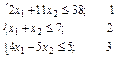
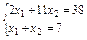D = –9; D1 = –39; D2 = –24;
