ЗАГАЛЬНА ПОСТАНОВКА ЗАДАЧІ
Необхідно знайти оптимум наступної функції:
Задача вирішується при обмеженнях виду:
Задача (3.10)–(3.11) може бути зведена до задачі лінійного програмування. Для цього необхідно ввести нові змінні, при цьому
З використанням нових змінних, задача (3.10)-(3.11) зводиться до наступної ЗЛП:
при обмеженнях виду:
і рівняннях зв'язків виду
Задача вирішується при умовах невід’ємності, що накладають на n змінних
Задача (3.12)-(3.15) є задачею лінійного програмування, отже, розв’язуючи її відомими методами можна знайти відповідні розв’язки. При цьому, одержавши оптимальний план такої задачі, на підставі співвідношень (3.12) можна знайти оптимальний план вихідної задачі (3.10)-(3.11). Таким чином, можна вказати наступний алгоритм розв’язування ЗДЛП. I. Вихідну ЗДЛП (3.10)-(3.11) зводять до ЗЛП (3.12)-(3.15). II. Знаходять оптимальний план ЗЛП відомими методами. III. Використовуючи співвідношення (3.12) знаходять оптимальний план вихідної задачі. IV. Підставляючи значення xj, при Приклад. Знайти максимальне значення функції:
Зведемо дану задачу до ЗЛП, при цьому
Далі вводимо нові змінні:
Тоді вихідна задача (3.16)-(3.18) зводиться до наступної ЗЛП
Задача вирішується в рамках обмежень виду:
Задача (3.19)-(3.22) є ЗЛП і розв’язок її можна знайти методом штучного базису. Для цього формулюють наступну розширену задачу
Далі розширену задачу заносять у первісну симплексну таблицю
Далі розділивши останню таблицю на 10, одержують оптимальний план ЗЛП
Висновок: у процесі визначення первісного опорного плану робоча точка пошуку экстремума вийшла в ту вершину опуклого багатогранника, що є точкою максимуму.
З урахуванням того, що
розв’язування задачі в середовищі Mathcad:
|

 (3.10)
(3.10)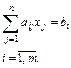 (3.10)
(3.10)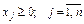 . (3.11)
. (3.11) . У такому випадку здійснюється перехід в область нових змінних, на підставі співвідношень виду:
. У такому випадку здійснюється перехід в область нових змінних, на підставі співвідношень виду: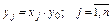 . (3.12)
. (3.12)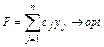 (3.12)
(3.12)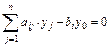 (3.13)
(3.13)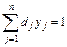 (3.14)
(3.14)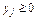 ;
; . (3.15)
. (3.15)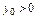 .
.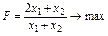 ; (3.16)
; (3.16)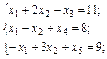 (3.17)
(3.17)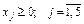 . (3.18)
. (3.18)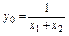 . (3.19)
. (3.19)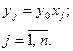 (3.20)
(3.20) . (3.19)
. (3.19)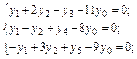 (3.20)
(3.20)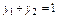 ; (3.21)
; (3.21)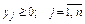 ; (3.22)
; (3.22)
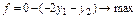 ;
; ;
;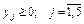 ;
;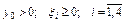 .
.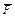
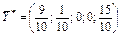
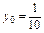 .
.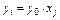 , знаходять оптимальний план ЗДЛП
, знаходять оптимальний план ЗДЛП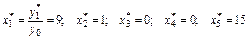
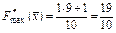 .
.


