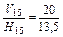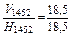Особливості методу гілок і границь для розв’язування задачі про комівояжера
Для методу гілок і границь існують різні підходи його реалізації. Однак загальною є ідея розбивки (розгалуження) множини припустимих значень (на дерево підмножин (дерево розв’язків). При цьому процес розгалуження, заснований на побудові оцінок знизу (нижньої границі) для цільової функції на деякій множині розв’язків. Для кожної задачі, з урахуванням її специфіки, розробляються наступні підходи: 1) Правило розгалуження. 2) Спосіб обчислення оцінок (функція цілі). 3) Способи знаходження розв’язків. Отже, основною особливістю методу гілок і границь є те, що він дозволяє організувати повну процедуру перебору відповідних планів задачі. Розглянемо зазначений підхід детально. Нехай на деякій множині W необхідно мінімізувати функцію j. Тоді цю процедуру реалізують у такий спосіб: W розбивають на ряд непересічних підмножин і потім вибирається та підмножина, наприклад W1, на якій функція j досягає свого найменшого значення. Далі розбивають W1 на ряд підмножин і вибирають ту з них, наприклад W2, на якій функція j досягає свого мінімального значення. Далі W2 розбивають на кілька непересічних частин. Такий процес розгалуження реалізують до одноелементної множини. Така одноелементна множина називається рекордом. Практичну реалізацію методу гілок і границь для задачі про комівояжера зручніше за все проводити на тлі конкретному прикладі. Приклад. Спекла бабка колобок і поставила його остигати на віконце. І вирішив колобок, що поки він стигне, він може оббігти ліс, подивитися на лісових жителів і знову повернутися. Сказано-зроблено. Зстрибнув він з віконця й покотився в ліс. Допоможіть колобку знайти найкоротший шлях його руху в лісі, якщо відстань між норами й будинком діда й баби дані в наступній таблиці:
Математична модель задачі: для рішення задачі привласнимо кожному пункту задачі певний номер: дід і баба = 1, заєць =2, вовк = 3, ведмідь = 4, лисиця = 5. Отже, загальне число пунктів n = 5. Тоді, на першому етапі можна записати функцію цілі задачі
Задача вирішується в рамках наступних обмежень: дозволяється перехід з 1 пункту в 2 або 3 або 4 або5
Розв’язування задачі комівояжера методом гілок і границь 1. Аналіз вихідної множини ((омега) Знайдемо оцінку знизу функції якості. Для цієї мети на першому етапі визначимо матрицю мінімальних відстаней по рядках
Далі знаходимо значення функції цілі
Аналогічно визначається матриця мінімальних відстаней по стовпцях
Тоді У такому випадку оцінка функції якості Н буде визначатися на основі співвідношення
Далі оцінимо верхнє значення функції якості. Для цієї мети виберемо початковий план
У такому випадку верхнє значення функції якості Очевидно, що вихідна множина планів (буде містити в собі наступні підмножини:
Тут W ij означає перехід з i-того пункту (у цьому випадку 1) в j-ий. 2. Аналіз підмножини W12
У такому випадку на першому етапі матрицю вихідних маршрутів можна представити у вигляді
Для визначення нижньої границі функції якості на підмножині W12 знову визначають мінімальне значення функції якості по рядках і стовпцях
3. Аналіз підмножини W13
Верхня оцінка функції якості на цій підмножині
4. Аналіз підмножини W14
Далі визначаємо верхню границю функції якості на цій підмножині
5. Аналіз підмножини W15
Визначимо нижнє значення функції якості на множині W15
6. Відсівання безперспективних підмножин
Підмножини V 12 й V 14 мають найкращу верхню оцінку функції якості, однак перспективним є підмножина W14, в силу того, що нижня границя функції якості є ближче до оптимальної. Отже, надалі необхідно розглядати підмножину W14. Розглядається підмножина W14, що містить у собі наступні підмножини 7. Аналіз підмножини W142
Далі обчислюють верхню границю функції якості
Визначення нижньої границі функції якості
8. Аналіз підмножини W143
Визначення верхньої границі функції якості
Визначення нижньої границі функції якості
9. Аналіз підмножини W145
Визначення верхньої границі функції якості
Визначення нижньої границі функції якості
10. Відсівання безперспективних підмножин
Підмножина V 143 є безперспективною.В силу того, що верхня границя функції якості на підмножинах V 142 й V 145 збігаються між собою, то далі порівнюють між собою нижні границі функції якості і тому що Н 142 > Н 145, то рекордом є підмножина W145. При цьому W145 буде містити в собі 2 непересічні підмножини 11. Аналіз підмножини W1452
Визначення верхньої границі функції якості
Визначення нижньої границі функції якості
12. Аналіз підмножини W1453
Визначення верхньої границі функції якості
Визначення нижньої границі функції якості
13. Відсівання безперспективних підмножин
14. У такому випадку
Оптимальна матриця переміщень буде представлена в такий спосіб
Таким чином, оптимальний маршрут колобка буде представлений наступними відвідуваннями: дід і баба ® ведмідь ® лисиця ® заєць ® вовк ® дід і баба. При цьому
Дерево розв’язків
|





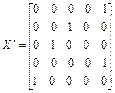
 .
. .
. .
. – вибираємо максимальне число.
– вибираємо максимальне число. .
. .
. .
.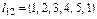
 .
.

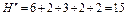








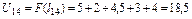



 .
.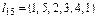

 . – можливий варіант відвідування
. – можливий варіант відвідування

 .
.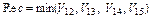 .
.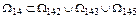 .
. .
. .
. . – можливі шляхи пересування комівояжера
. – можливі шляхи пересування комівояжера

 .
.


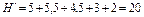
 .
.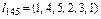




 .
.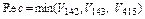 .
. .
.




 .
.




 .
. .
. .
.
 .
.