ГРАФІЧНИЙ МЕТОД розв’язування ЗДЛП
Постановка задачі Необхідно знайти экстремум наступної функції
і умовах невід’ємності, що накладають на змінні:
Аналіз задачі (3.4)-(3.6) 1. Областю припустимих розв’язків задачі (3.4)–(3.6) служить або замкнуте опукле багатогранне тіло або розімкнуте опукле багатогранне тіло. Таке тіло визначається системою обмежень (3.5) і умовами невід’ємності (3.6), які накладаються на змінні х 1, х 2. 2. Функція (3.4) визначає в площині Х1 0 Х2 сімейство прямих, що проходять через початок координат. Таке сімейство прямих описується рівняннями виду:
3. Обертаючи пряму (3.4) відносно початку координат, можна знайти ту вершину ОПР, в якій функція (3.4) досягає свого оптимального значення (якщо таке значення існує). Крім того, при обертанні такої прямої можна переконатися в нерозв'язності задачі (3.4)-(3.6). Алгоритм розв’язування задачі (3.4)-(3.6) 1. У площині Х1 0 Х2 будуємо область припустимих розв’язків задачі, що визначається співвідношеннями (3.5)–(3.6). Помітимо, що якщо така область замкнута, то задача (3.4)-(3.6) завжди має рішення.
2. У площині Х1 0 Х2 будуємо пряму лінію з рівнянням 3. Обертаючи пряму відносно початку координат, визначаємо крайню точку ОПР або переконуємося в нерозв'язності такої задачі. У розглянутій задачі 4. Далі визначаємо координати точки оптимуму й підставляємо їх у вираз для функції мети. Розглянемо приклад. Приклад. Для виробництва двох видів виробів А й В підприємство використовує три типи технологічного встаткування. Кожен виріб повинен пройти обробку на кожному типі встаткування. Час обробки виробу на кожнім устаткуванні наведено в таблиці. Крім того, в таблиці зазначені витрати, пов'язані з виробництвом одного виробу кожного виду
Підприємство може використати встаткування першого й третього типів не більше 26 й 39 годин відповідно. При цьому встаткування другого типу доцільно використовувати не менше 4 годин. Потрібно визначити, скільки виробів кожного виду варто виготовляти даному підприємству, щоб собівартість кожного виробу була мінімальною. Сформулюємо задачу математично. Позначимо через х 1 і х 2 кількість виробів видів А и В відповідно, який повинне виготовляти дане підприємство при мінімальних загальних витратах Тоді функція, відповідальна за собівартість одного виробу, визначається співвідношенням:
Задача розв’язується в рамках наступних обмежень
Висновок: 1) математична постановка задачі складається у визначенні такого невід’ємного розв’язку системи обмежень (3.8), що доставляє мінімум функції (3.7); 2) беручи до уваги, що математична модель (3.7)–(3.9) містить у собі лише дві змінні, задача може бути вирішена графічно в площині Х 10 Х 2.
В силу того, що область замкнута, вихідна ЗДЛП завжди буде мати розв’язок. Зобразимо в площині Х1 0 Х2 рівняння прямої Виразимо із цього рівняння х 2:
Очевидно, що при збільшенні h кутовий коефіцієнт буде рости (отже, буде збільшуватися й відповідна похідна). Стрілки на графіку вказують напрямок збільшення h, отже, максимум цільової функції буде досягнутий у точці А, а мінімум – у точці В. Визначимо координати точки В із системи рівнянь:
Отже, оптимальним планом виробництва є план, при якому підприємство буде виготовляти три вироби виду А и один виріб виду В. При цьому собівартість одного виробу складе 2, 25 грошових одиниць, тобто
|

 (3.4), при обмеженнях виду:
(3.4), при обмеженнях виду: (3.5)
(3.5) . (3.6)
. (3.6) .
.

 .
. . (3.7)
. (3.7) (3.8)
(3.8) (3.9)
(3.9)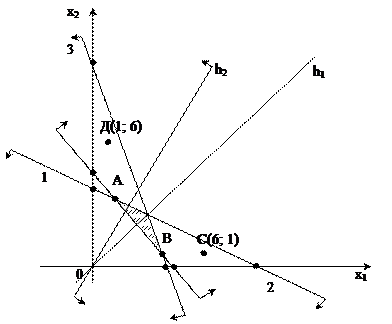
 .
. .
. . Одержимо
. Одержимо 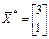 .
.



