ДЛЯ ПІДСУМКОВОГО КОНТРОЛЮ ЗНАНЬ
1. Математична модель операції. Загальна постановка задачі дослідження операцій. 2. Класифікація моделей і методів дослідження операцій. Приклади|приклады| задач, які|какие| вирішуються методами дослідження операцій. 3. Задача планування виробництва і її математична модель. 4. Задача складання|складывания, сдачи| раціону (задачі про дієту й суміші) і особливість її математичної моделі. 5. Математична модель задачі про завантаження встаткування. 6. Математичні моделі задач розкрою матеріалу. 7. Аналіз математичних моделей з погляду ефективних методів їхнього рішення|решения|. 8. Використання цілочисельних задач ЛП| у плануванні й керуванні виробництвом і їхньою математичною постановкою. 9. Методи Гоморри. 10. Метод гілок і границь|. 11. Класичний метод оптимізації задач НП.| Метод невизначених множників Лагранжа, економічна|экономичная| інтерпретація. 12. Теорема Куна-Такера. 13. Метод найшвидшого спуска. 14. Метод сполучених градієнтів Флетчера-Ривса. 15. Метод Давидона-Флетчера-Пауела (ДФП|). 16. Методи випадкового пошуку з лінійною й нелінійною тактиками. 17. Мережна модель і її основні елементи. Порядок і правила побудови сіткових графіків. 18. Системи масового обслуговування (СМО|). Основні поняття й визначення. Класифікація СМО|. 19. Поняття про статистичне моделювання СМО| (метод Монте-Карло). 20. Моделі керування запасами. |припасами|..
1. ЦІЛОЧИСЕЛЬНЕ ЛІНІЙНЕ ПРОГРАМУВАННЯ (ЦЛП) ЦЛП - це розділ дослідження операцій, що орієнтований на рішення задач, у яких всі змінні або частина з них є цілочисельними (повністю або частково цілочисельні задачі). Класичним прикладом цілочисельних задач лінійного програмування (ЦЗЛП) є задача, що у літературі називається задачею комівояжера. Ця задача формулюється в такий спосіб. Комівояжер повинен відвідати ряд міст, відстані між якими відомі. Комівояжер вибирає самий короткий замкнутий маршрут, що починається й закінчується в місті його проживання, при цьому він повинен відвідати необхідне місто один і тільки один раз. Очевидно, що завдання комівояжера полягає в оптимальному виборі його маршруту. Іншою класичною задачею такого типу є задача про ранець. Розглянемо формулювання цієї задачі. Є n предметів, при цьому відомо: aj – вага j-ого предмета, cj - цінність j-ого предмета, А – вантажопідйомність ранця. Необхідно завантажити ранець набором предметів максимальної цінності. Складемо математичну модель задачі про ранець. На першому етапі введемо змінні:
У такому випадку функція цілі буде мати такий вигляд:
Задача вирішується в рамках наступних обмежень:
У деяких інших моделях такої задачі можуть фігурувати й інші обмеження, наприклад, сумарний об'єм ранця, габарити предметів і т.д. У загальному випадку ЗЦЛП формулюється в такий спосіб: знайти оптимальний план
Задача вирішується в рамках обмежень:
Якщо в обмеженні (6) j змінюється в межах Відомо, що экстремум ЗЛП досягається у вершинах опуклого багатогранного тіла, що є ОДР (областю припустимих рішень) задачі. Для ЦЗЛП значення экстремуму може досягатися в будь-якій вершині ОПР. Це означає, що методи розв’язування ЗЛП у раніше освітленому виді (у курсі математичного програмування) не можуть бути застосовані для рішення ЦЗЛП. Проілюструємо сказане геометрично.
З малюнка видно, що цілочисельний розв’язок може досягатися в будь-якій точці опуклого багатогранника. Отже, для рішення ЦЗЛП необхідно розглядати спеціальні методи. Такі методи діляться на три основні групи: I група - методи відсікання; II група - комбінаторні методи (методи розсічення); III група - наближені методи. У методах даної групи використовуються два основних підходи: - розробка детермінованих евристичних алгоритмів, які враховують специфіку конкретної задачі; - застосування спрямованого випадкового пошуку з локальною оптимізацією.
|


 (1)
(1) , (2)
, (2)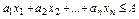 .
. , що забезпечує досягнення цільовою функцією екстремального значення:
, що забезпечує досягнення цільовою функцією екстремального значення: . (3)
. (3) (4)
(4) (5)
(5) (6)
(6) , то вихідна задача називається повністю цілочисельною, якщо ж
, то вихідна задача називається повністю цілочисельною, якщо ж  а
а  , те задачу називають частково цілочисельною.
, те задачу називають частково цілочисельною.



