РІШЕННЯ ЗАДАЧІ ПРО КОМІВОЯЖЕРА МЕТОДОМ гілок І ГРАНИЦЬПостановка задачі Є n міст (А 1, А 2, А 3,... Аn), задана матриця відстаней між містами Математична модель задачі У загальному випадку нехай розглядаються n пунктів, тоді вводиться n 2 альтернативних змінних xij. Причому відповідна змінна буде дорівнювати 0, якщо перехід з i в j пункт не входить у розглянутий маршрут. І, мабуть, що така змінна буде дорівнювати 1, якщо зазначений перехід можливий. Тоді умова прибуття в кожен пункт і виходу з кожного пункту тільки по одному разу виражається співвідношенням виду:
Для забезпечення безперервності маршруту вводять додатково n змінних
У такому випадку сумарна довжина маршруту, який необхідно мінімізувати, буде записуватися в наступному вигляді:
Для розв’язування задачі (4.1)–(4.4) існує багато різних методів. Однак, одним з найбільш, простих і зручних є метод гілок і границь.
|
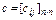. Необхідно відшукати такий найкоротший замкнутий маршрут (цикл), що проходить один і тільки один раз через кожне місто, при якому мінімізується сумарна довжина шляху 
.
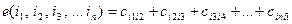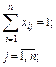(4.1)
(4.2)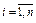
і при цьому формують n 2 додаткових обмежень:
;
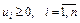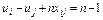. (4.3)
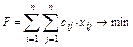. (4.4)
