Алгоритм методу гілок і границь
1. На множині припустимих планів G 0 знаходять оптимальне значення функції цілі (2.1), відкинувши умови цілочисельності (2.4). При цьому знаходять оцінку функції якості
Цю оцінку вважають верхньою оцінкою функції якості G 0. Якщо план Якщо ж умови цілочисельності для задачі (2.1)-(2.4) не виконуються, то переходять до пункту два цього алгоритму. 2. Починають розвивати процес розгалуження. Для цього вибирають деяку нецілочисельну компоненту xj = xj 0, 1 £ j £ n. При цьому множину G 0 розбивають на дві непересічні підмножини Операцію реалізують у такий спосіб
3. На третьому етапі розв’язуються дві задачі лінійного програмування. Одна – на множині Якщо ж, допустимо, на множині 4. Далі здійснюють процес розгалуження ОПР і паралельно формують дерево розв’язків. Процес розгалуження реалізують доти, поки не знайдуть той оптимальний план, що задовольняє постановці задачі. Після того, як дерево розв’язків буде сформовано остаточно, аналізують кожну його гілку і знаходять той вектор
|
.
задовольняє умовам цілочисельності, то він вважається оптимальним для ЦЗЛП (2.1)–(2.4).
.
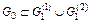Для наочності отриманого результату зображують дерево розв’язків.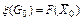
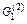
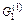, а друга – на множині 
, то надалі розвивається процедура розгалуження на множині 
, що доставляє оптимум функції якості (2.1).
