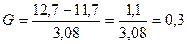Середнє квадратичне відхилення
Додатковою характеристикою середньої арифметичної, що показує мінливість, є середнє квадратичне відхилення G варіаційного ряду. Чим менше G, тим більш однорідний варіаційний ряд (стабільні ознаки, показник і результат). Середнє квадратичне відхилення застосовується при оцінці мінливості варіаційного ряду, обчисленні коефіцієнту варіації, оцінці фізичного розвитку, визначенні середніх помилок і розміру вибірки. На основі теорії розподілу для статистичних сукупностей розроблено елементарний спосіб визначення середнього квадратичного відхилення
де Vmax — найбільше значення варіанти; Vmin — найменше; К — коефіцієнт кількості випадків. Наприклад, у бігові на 100 м кращий результат 11, 7 с (Vmax), а гірший — 12, 7 с (Vmin). Коефіцієнт К згідно таблиці 1 дорівнює для десяти випадків 3, 08. Підставляємо у формулу числові значення і визначаємо середнє квадратичне відхилення.
Прийнято вважати, що всі індивідуальні показники у межах ±1 G оцінюються як «норма» і носять випадковий характер. Показники ±2 G носять невипадковий характер, а ±3 G мають значне відхилення від норми.
|