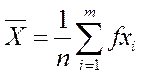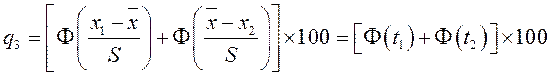Теоретическая часть. Взяв выборку из генеральной совокупности и вычисляя статистические характеристики этой выборки - X и S
Взяв выборку из генеральной совокупности и вычисляя статистические характеристики этой выборки - X и S, можно с некоторой приближенностью считать, что эти характеристики по своим величинам будут близки к соответствующим параметрам генеральной совокупности – X0 и σ 0, т.е. это их оценки.
Если
X0 ≈ X, σ 0 ≈ S,
где X0, X – среднеарифметические значения случайной величины соответственно в генеральной совокупности и в выборке объема n;
σ 0 , S – среднеквадратичные отклонения изучаемой величины соответственно генеральной совокупности и в выборке из нее,
то по заданной точности ε и вероятности α приближенного равенства σ 0 ≈ S можно определить необходимый объем выборки
n ≥ t2 / 2q2, (1)
где t определяется в зависимости от вероятности α, q = ε / σ;.
Значения t, q и α задает преподаватель. По этим величинам определяется объем выборки.
Затем студенты измеряют параметр X. При этом необходимо, чтобы цена деления шкалы измерительного инструмента была бы равна (1/6, …, 1/10) 2d, где 2d – допуск на размер детали.
Результаты измерений записываются в табл. 1.
Таблица 1
Результаты измерений
Далее необходимо обработать статистические данные. Находится наибольшее Xmax и наименьшее Xmin значения наблюдаемого параметра X.
Размах варьирования или широта распределения при этом составляет
Xmax - Xmin. (2)
Задав число интервалов n (m 7 при n = 5 – 100, m = 9 – 15 при n 100), определяем цену интервала:
C = (Xmax - Xmin)/ m (3)
Цена интервала должна быть больше (или равна) цены деления шкалы измерительного инструмента или прибора, что компенсирует погрешность измерения. Подсчет частот по каждому интервалу удобно производить следующими способами. Слева выписывают интервалы от Xmin до Xmin+С; от Xmin+С до Xmin+2С и т.д. В каждый интервал включают размеры, лежащие в пределах от наименьшего значения интервала включительно, до наибольшего значения интервала, исключая его. Справа при помощи черточек подсчитывают число размеров по интервалам (табл. 2).
Таблица 2.
Расчет числа размеров по интервалам
| Интервалы
| Подсчет частот
| Частота f
| | От
| до
| | Xmin
Xmin+С
…
…
| Xmin+С
Xmin+2С
…
Xmax
| | | |
| | | | | |
…
| |
|
…
Σ fi = n
|
По данным таблицы 2 вычерчивают эмпирическую (экспериментальную) кривую распределения (по оси абсцисс откладывают середины интервалов, по оси ординат – частоты). На основании таблицы частот и эмпирической кривой распределения выдвигается гипотеза о распределении случайной величины. В нашем случае правомерна гипотеза о нормальном распределении, которое часто применяется при решении задач математической статистики и статического контроля качества. Такое распределение свидетельствует об устойчивости технологического процесса, так как замеры со значительными отклонениями от номинального размера встречаются редко. Выдвинутую гипотезу необходимо проверить.
Чтобы найти и проверить закон распределения студенты рассчитывают числовые характеристики:
· cреднеарифметическое отклонение по формуле
(4)
· среднеквадратичное отклонение по формуле
(5)
где n – объем выборки;
xi – найденные размеры.
Вычисление среднеарифметического и среднеквадратичного отклонения при наличии обширных рядов измерений всегда трудоемко. Поэтому на практике для расчета этих статистических характеристик составляют таблицу предварительной обработки данных (табл. 3).
Таблица 3.
Расчет статистических характеристик измеряемых величин
| Интервал
| Середина интервала Xi
| Частота fi
| fi Xi
| (xi – x)
| (xi– x)2
| fi(xi– x)2
| | от
| До
|
|
|
|
|
|
| |
|
|
|
Σ fi
|
Σ fi Xi
|
|
|
Σ fi(xi– x)2
|
Тогда вместо формулы (4) можно воспользоваться формулой (6):
а вместо формулы (5) можно делать расчеты по формуле
(7)
Теперь следует проверить гипотезу нормальности распределения совокупности, из которой была взята выборка. Для этого нужно составить вспомогательную таблицу для вычисления критерия λ (табл. 4).
Таблица 4.
Промежуточные расчеты
| Середина разряда Xi
| t
| Zt
| f=(nc/S) Zt
| f
| Nx’
| Nx
| | Nx’- Nx |
| |
|
|
|
|
|
|
|
|
В таблице значение t вычислено по формуле:
(8)
Значения Zt взяты из таблицы 5.
Таблица 5.
Нормальное распределение вероятностей
| T
| Zt
| t
| Zt
| t
| Zt
| | 0, 0
| 0, 3989
| 1, 4
| 0, 1497
| 2, 8
| 0, 0070
| | 0, 1
| 0, 2980
| 1, 5
| 0, 1295
| 2, 9
| 0, 0060
| | 0, 2
| 0, 3910
| 1, 6
| 0, 1109
| 3, 0
| 0, 0044
| | 0, 3
| 0, 3814
| 1, 7
| 0, 0940
| 3, 1
| 0, 0033
| | 0, 4
| 0, 3683
| 1, 8
| 0, 0790
| 3, 2
| 0, 0024
| | 0, 5
| 0, 3521
| 1, 9
| 0, 0656
| 3, 3
| 0, 0017
| | 0, 6
| 0, 3332
| 2, 0
| 0, 0540
| 3, 4
| 0, 0012
| | 0, 7
| 0, 3123
| 2, 1
| 0, 0440
| 3, 5
| 0, 0009
| | 0, 8
| 0, 2897
| 2, 2
| 0, 0355
| 3, 6
| 0, 0006
| | 0, 9
| 0, 2661
| 2, 3
| 0, 0289
| 3, 7
| 0, 0004
| | 1, 0
| 0, 2420
| 2, 4
| 0, 0224
| 3, 8
| 0, 0003
| | 1, 1
| 0, 2179
| 2, 5
| 0, 0175
| 3, 9
| 0, 0002
| | 1, 2
| 0, 1942
| 2, 6
| 0, 0136
|
|
| | 1, 3
| 0, 1714
| 2, 7
| 0, 0104
|
|
|
Значение nc/S постоянно для всех значений Zt. Определяется f’ - теоретическая частота. По теоретическим частотам f’ строится теоретическая кривая распределения в том же масштабе, что был принят для построения эмпирической кривой. Совмещая эмпирическую и теоретическую кривые распределения, можно предварительно оценить близость эмпирического распределения к предлагаемому теоретическому. Для более точной оценки нужно вычислить Nx и Nx’ – накопленные эмпирические и теоретические частоты, прибавляя к каждому значению fi и f’ суммы предшествующих значений fi-1 или f’i-1.
Критерий λ находится по формуле:
(9)
По таблице 6 находится P (λ).
Таблица 6.
Определение вероятности критерия λ
| λ
| P (λ)
| λ
| P (λ)
| λ
| P (λ)
| | 0, 30
| 1, 0000
| 0, 80
| 0, 5441
| 1, 60
| 0, 0120
| | 0, 35
| 0, 9997
| 0, 85
| 0, 4653
| 1, 70
| 0, 0062
| | 0, 40
| 0, 9972
| 0, 90
| 0, 3927
| 1, 80
| 0, 0032
| | 0, 45
| 0, 9874
| 0, 95
| 0, 3275
| 1, 90
| 0, 0015
| | 0, 50
| 0, 9639
| 1, 00
| 0, 2700
| 2, 00
| 0, 0007
| | 0, 55
| 0, 9228
| 1, 10
| 0, 1777
| 2, 10
| 0, 0003
| | 0, 60
| 0, 8643
| 1, 20
| 0, 1122
| 2, 20
| 0, 0001
| | 0, 65
| 0, 7920
| 1, 30
| 0, 0681
| 2, 30
| 0, 0000
| | 0, 70
| 0, 7112
| 1, 40
| 0, 0397
| 2, 40
| 0, 0000
| | 0, 75
| 0, 6272
| 1, 50
| 0, 0222
| 2, 50
| 0, 0000
|
Если вероятность P (λ) окажется очень малой (практически, когда P (λ)≤ 0, 05), то расхождение эмпирического и теоретического распределения считается существенным, а не случайным, и гипотеза о нормальности закона распределения величины X отвергается.
Процент возможного брака определяется из сопоставления X, S и заданных границ допуска x1, x2.
Процент возможного брака по верхнему пределу:
(10)
Процент возможного брака по нижнему пределу:
(11)
Вероятное количество годных изделий в партии
(12)
где Φ (t1) – нормированная функция Лапласа (находится по табл. 7);
x1, x2 – соответственно верхняя и нижняя границы поля допуска.
Таблица 7.
Нормированная функция Лапласа
| t
| Φ (t)
| t
| Φ (t)
| t
| Φ (t)
| | 0, 00
| 0, 0000
| 0, 74
| 0, 2704
| 1, 48
| 0, 4306
| | 0, 02
| 0, 0008
| 0, 76
| 0, 2764
| 1, 50
| 0, 4332
| | 0, 04
| 0, 0016
| 0, 78
| 0, 2823
| 1, 52
| 0, 4357
| | 0, 06
| 0, 0024
| 0, 80
| 0, 2881
| 1, 54
| 0, 4382
| | 0, 08
| 0, 0032
| 0, 82
| 0, 2939
| 1, 56
| 0, 4406
| | 0, 10
| 0, 0040
| 0, 84
| 0, 2995
| 1, 58
| 0, 4429
| | 0, 12
| 0, 0048
| 0, 86
| 0, 3051
| 1, 60
| 0, 4452
| | 0, 14
| 0, 0557
| 0, 88
| 0, 3106
| 1, 62
| 0, 4474
| | 0, 16
| 0, 0636
| 0, 90
| 0, 3159
| 1, 64
| 0, 4495
| | 0, 18
| 0, 0714
| 0, 92
| 0, 3212
| 1, 66
| 0, 4515
| | 0, 20
| 0, 0793
| 0, 94
| 0, 3264
| 1, 68
| 0, 4533
| | 0, 22
| 0, 0871
| 0, 96
| 0, 3315
| 1, 70
| 0, 4554
| | 0, 24
| 0, 0948
| 0, 98
| 0, 3365
| 1, 72
| 0, 4573
| | 0, 26
| 0, 1026
| 1, 00
| 0, 3412
| 1, 74
| 0, 4591
| | 0, 28
| 0, 1103
| 1, 02
| 0, 3461
| 1, 76
| 0, 4608
| | 0, 30
| 0, 1179
| 1, 04
| 0, 3508
| 1, 78
| 0, 4625
| | 0, 32
| 0, 1255
| 1, 06
| 0, 3554
| 1, 80
| 0, 4661
| | 0, 34
| 0, 1331
| 1, 08
| 0, 3599
| 1, 82
| 0, 4656
| | 0, 36
| 0, 1406
| 1, 10
| 0, 3643
| 1, 84
| 0, 4671
| | 0, 38
| 0, 1480
| 1, 12
| 0, 3686
| 1, 86
| 0, 4688
| | 0, 40
| 0, 1554
| 1, 14
| 0, 3729
| 1, 88
| 0, 4699
| | 0, 42
| 0, 1628
| 1, 16
| 0, 3770
| 1.90
| 0, 4713
| | 0, 44
| 0, 1700
| 1, 18
| 0, 3810
| 1, 92
| 0, 4726
| | 0, 46
| 0, 1772
| 1, 20
| 0, 3849
| 1, 94
| 0, 4738
| | 0, 48
| 0, 1844
| 1, 22
| 0, 3888
| 1, 96
| 0, 4750
| | 0, 50
| 0, 1915
| 1, 24
| 0, 3925
| 1, 98
| 0, 4761
| | 0, 52
| 0, 1985
| 1, 26
| 0, 3962
| 2, 00
| 0, 4772
| | 0, 54
| 0, 2054
| 1, 28
| 0, 3997
| 2, 02
| 0, 4783
| | 0, 56
| 0, 2123
| 1, 30
| 0, 4032
| 2, 04
| 0, 4793
| | 0, 58
| 0, 2190
| 1, 32
| 0, 4066
| 2, 06
| 0, 4803
| | 0, 60
| 0, 2257
| 1, 34
| 0, 4099
| 2, 08
| 0, 4812
| | 0, 62
| 0, 2324
| 1, 36
| 0, 4131
| 2, 10
| 0, 4821
| | 0, 64
| 0, 2389
| 1, 38
| 0, 4162
| 2, 12
| 0, 4830
| | 0, 66
| 0, 2454
| 1, 40
| 0, 4192
| 2, 14
| 0, 4838
| | 0, 68
| 0, 2517
| 1, 42
| 0, 4222
| 2, 16
| 0, 4846
| | 0, 70
| 0, 2580
| 1, 44
| 0, 4251
| 2, 18
| 0, 4854
| | 0, 72
| 0, 2642
| 1, 46
| 0, 4279
| 2, 20
| 0, 4861
| | 2, 22
| 0, 4868
| 2, 48
| 0, 4934
| 2, 78
| 0, 4973
| | 2, 24
| 0, 4875
| 2, 50
| 0, 4938
| 2, 82
| 0, 4976
| | 2, 26
| 0, 4881
| 2, 52
| 0, 4941
| 2, 86
| 0, 4979
| | 2, 28
| 0, 4887
| 2, 54
| 0, 4945
| 2, 90
| 0, 4981
| | 2, 30
| 0, 4893
| 2, 56
| 0, 4948
| 3, 00
| 0, 4986
| | 2, 32
| 0, 4898
| 2, 58
| 0, 4951
| 3, 20
| 0, 4993
| | 2, 34
| 0, 4904
| 2, 60
| 0, 4953
| 3, 40
| 0, 4996
| | 2, 36
| 0, 4909
| 2, 62
| 0, 4956
| 3, 60
| 0, 4998
| | 2, 38
| 0, 4913
| 2, 64
| 0, 4959
| 3, 80
| 0, 499929
| | 2, 40
| 0, 4918
| 2, 66
| 0, 4961
| 4, 00
| 0, 499968
| | 2, 42
| 0, 4922
| 2, 68
| 0, 4963
| 4, 50
| 0, 499997
| | 2, 44
| 0, 4927
| 2, 70
| 0, 4965
| 5, 00
| 0, 499999
| | 2, 46
| 0, 4931
| 2, 74
| 0, 4969
|
|
|
Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|
Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|
Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|
Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|
|
Признаки классификации безопасности Можно выделить следующие признаки классификации безопасности.
1. По признаку масштабности принято различать следующие относительно самостоятельные геополитические уровни и виды безопасности.
1.1. Международная безопасность (глобальная и...
Прием и регистрация больных Пути госпитализации больных в стационар могут быть различны. В центральное приемное отделение больные могут быть доставлены:
1) машиной скорой медицинской помощи в случае возникновения острого или обострения хронического заболевания...
ПУНКЦИЯ И КАТЕТЕРИЗАЦИЯ ПОДКЛЮЧИЧНОЙ ВЕНЫ
Пункцию и катетеризацию подключичной вены обычно производит хирург или анестезиолог, иногда — специально обученный терапевт...
|
|
Основные структурные физиотерапевтические подразделения Физиотерапевтическое подразделение является одним из структурных подразделений лечебно-профилактического учреждения, которое предназначено для оказания физиотерапевтической помощи...
Почему важны муниципальные выборы? Туристическая фирма оставляет за собой право, в случае причин непреодолимого характера, вносить некоторые изменения в программу тура без уменьшения общего объема и качества услуг, в том числе предоставлять замену отеля на равнозначный...
Тема 2: Анатомо-топографическое строение полостей зубов верхней и нижней челюстей. Полость зуба — это сложная система разветвлений, имеющая разнообразную конфигурацию...
|
|
