Направление химического процесса
Второе начало термодинамики утверждает, что в изолированной системе самопроизвольно протекают процессы, приводящие к увеличению энтропии, которые прекращаются при достижении ее максимального значения, соответствующего состоянию равновесия. Таким образом, условием самопроизвольного протекания неравновесного процесса является Поскольку температура Т – величина всегда положительная, то в общем виде можно написать: Рассмотрим применение полученного неравенства к часто встречающимся на практике процессам. Изобарно-изотермический процесс (p –const, Т –const). Поскольку в изобарном процессе d Qp = dH, то dH – T × dS £ 0. При постоянной температуре d (H – T × S)£ 0. Выражение под знаком дифференциала заменяется функцией G º H – T × S. Тогда очевидно, что условием самопроизвольного протекания изобарно-изотермического процесса будет dG < 0 ( D G < 0), а условием равновесия dG =0 (D G =0). G – функция состояния системы, получившая название энергии Гиббса (Gibbs). Энергия Гиббса – это часть энергии системы, которая может быть отдана ею в изобарно-изотермическом процессе в виде теплоты или работы без разрушения самой системы. Размерность величины энергии Гиббса [Дж, кДж], для единицы количества вещества [Дж/моль, кДж/моль]. Так же как и для всех функций состояния, содержащих в себе внутреннюю энергию, ее абсолютное значение неопределимо. Поэтому пользуются величиной изменения энергии Гиббса: D G =D H – T × D S. Для индивидуальных веществ в стандартном термодинамическом состоянии величины энергии Гиббса их образования D fG 0298, соответствующие ее изменению в реакции образования сложного вещества из простых, приведены в справочной литературе. Для определения термодинамической возможности самопроизвольного протекания химической реакции необходимо рассчитать изменение энергии Гиббса (D rG 0298). Поскольку энергия Гиббса является функцией состояния, то ее изменение равно разности между суммами энергий Гиббса образования продуктов реакции и исходных веществ с учетом числа молей реагирующих веществ: D rG 0298=(å n i × D fG 0 i)продукты–(å n i × D fG 0 i)исх. вещества для реакции n аA + n bB = n сC + n dD D rG 0298=(n c × D fG 0 C + n d × D fG 0 D)–(n a × D fG 0 A + n b × D fG 0 B). Очевидно, что Для химической реакции стандартное изменение энергии Гиббса можно определить, зная стандартные энтальпии образования и энтропии исходных веществ и продуктов реакции: D rG 0298=(å n i × D fG 0 i)продукты–(å n i × D fG 0 i)исх. вещества= = [å n i × (D fH 0298 i –298× S 0298 i ]продукты–[å n i (D fH 0298 i –298× S 0298 i ]исх. вещества. Если раскрыть скобки и сгруппировать однородные члены, то получим D rG 0298=[(å n i × D fН 0 i)прод.–(å n i × D fН 0 i)исх. в.]–298× [(å n i × S 0 i)прод. –(å n i × S 0 i)исх. в.]. Учитывая, что (å n i × D fН 0 i)прод. – (å n i × D fН 0 i)исх.в = D rH 0, (å n i × S 0 i)прод. – D rG 0298=D rH 0298–298 × D rS 0298. Таким образом, направление самопроизвольного протекания химической реакции определяют два фактора: энтальпийный и энтропийный. Самопроизвольному протеканию способствует, с одной стороны, уменьшение энтальпии (D rH 0< 0, стремление к минимуму энергии), с другой – увеличение энтропии (D rS 0> 0, стремление системы к беспорядку). Энтальпия (D rH 0) и энтропия (D rS 0) реакции могут быть как положительными, так и отрицательными величинами. Таким образом, термодинамическая возможность самопроизвольного протекания химических реакций будет определяться соотношением энтальпийного и энтропийного факторов. В большинстве случаев химические реакции осуществляют не при стандартной (298 К), а при некоторой температуре Т. В этом случае термодинамическое условие их самопроизвольного протекания будет определяться температурной зависимостью величины энергии Гиббса: D rG 0(Т)=D rH 0(Т)– T× D rS 0(Т) < 0. На практике для оценки этой зависимости приближенно можно считать, что D rG 0(Т)»D rH 0298– T× D rS 0298< 0. Проанализируем влияние температуры на величину изменения энергии Гиббса для реакций с различным соотношением их энтальпии и энтропии. 1. Экзотермическая реакция (D rH 0< 0): · если энтропия в ходе реакции возрастает (D rS 0> 0), то оба фактора (энтальпийный и энтропийный) благоприятствуют ее протеканию. Химическая реакция может самопроизвольно протекать при любой температуре; · если энтропия в ходе реакции уменьшается (D rS 0< 0), то энтальпийный фактор благоприятствует ее протеканию, а энтропийный противодействует. Химическая реакция может самопроизвольно протекать только в том случае, если ï T× D rS 0ï < ê D rH 0ê, что выполняется при условии Примечание. Поскольку абсолютная величина теплового эффекта реакции обычно составляет порядка сотен кДж/моль, а изменение энтропии в ходе реакции – порядка десятков Дж/моль× K, то большинство экзотермических реакций при стандартной температуре протекает самопроизвольно. 2. Эндотермическая реакция (D rH 0> 0): · если энтропия в ходе реакции возрастает (D rS 0> 0), то энтальпийный фактор противодействует, а энтропийный способствует ее протеканию. Химическая реакция самопроизвольно может протекать только в том случае, если ï T× D rS 0ï > ê D rH 0 ê, что выполняется при условии · если энтропия в ходе реакции уменьшается (D rS 0< 0), то оба фактора препятствуют ее протеканию. Термодинамика запрещает самопроизвольное протекание таких реакций, поскольку при любых температурахD rG 0> 0. Примеры. 1. Определить направление самопроизвольного протекания реакции взаимодействия оксида кальция и воды с образованием дигидроксида кальция в стандартных условиях: CaO(кр) + H2O(ж) = Ca(OH)2(кр) D fG 0298, кДж/моль –603, 46 –237, 23 –897, 52 D fH 0298, кДж/моль –635, 09 –285, 83 –985, 12 S 0298, Дж/моль× K 38, 07 69, 95 83, 39 Решение. Направление самопроизвольного протекания реакции определяется по изменению энергии Гиббса (D rG 0< 0). а) Зная величины D fG 0 для реагентов, можно непосредственно вычислить изменение энергии Гиббса в ходе реакции: D rG 0298= (å n i × D fG 0 i) продукты–(å n i × D fG 0 i )исх. вещества, D rG 0298 = (1× (–897, 52)) – (1× (–603, 46) + 1× (–237, 23)) = –56, 83 (кДж). Следовательно, данная реакция в стандартных условиях может самопроизвольно протекать в прямом направлении. б) Изменение энергии Гиббса можно также вычислить по тепловому эффекту и энтропии реакции: D rG 0298 = D rН 0298 –298× D rS 0298, D rН 0298 = (å n i × D fН 0298 i )продукты – (å n i × D fН 0298 i )исх. вещества, D rS 0298 = (å n i × S 0298 i )продукты – (å n i × S 0298 i ) исх. вещества, D rН 0298 = (1× (–985, 12)) – (1× (–635, 09) + 1× (–285, 83)) = –64, 2 (кДж), D rS 0298 = (1× 83, 39) – (1× 38, 07 + 1× 69, 95) = –24, 63 (Дж/× K), D rG 0298 = –64, 2 – 298× (–24, 63× 10-3) = –56, 86 (кДж). Результаты первого и второго расчетов, естественно, совпадают (с учетом погрешности). 2. Определить возможность самопроизвольного окисления ртути кислородом в стандартных условиях (прямая реакция) и температуру, при которой возможен самопроизвольный распад окиси ртути на ртуть и кислород (обратная реакция): Hg(ж) + ½ O2(газ) = HgO(кр) D fH 0298, кДж/моль 0 0 –90, 88 S 0298, Дж/моль× K 75, 90 205, 04 70, 29 Решение. Изменение энергии Гиббса в ходе реакции вычисляют по тепловому эффекту и энтропии реакции при Т=298 К: D rG 0(Т)» D rН 0298 – Т × D rS 0298, D rН 0298 = (å n i × D fН 0298 i )продукты – (å n i × D fН 0298 i )исх. вещества, D rS 0298 = (å n i × S 0298i)продукты – (å n i × S 0298 i ) исх. вещества, D rН 0298 = 1× (–90, 88) – (1× 0 +½ × 0) = –90, 88 кДж/моль, D rS 0298 = 1× 70, 29 – (1× 75, 90 +½ × 205, 04) = –108, 13 Дж/моль× K, D rG 0298 = –90, 88 – 298× (–108, 13× 10-3) = –58, 65 кДж/моль. Поскольку D rG 0298< 0, то окисление ртути в стандартных условиях возможно. Самопроизвольное разложение окиси ртути на кислород и ртуть возможно, если Примечание. Необходимо отметить, что использование стандартной энергии Гиббса для определения направления химической реакции относится к идеальному процессу. Условием для полного превращения исходных веществ в продукты в реальном химическом процессе является D rG 0< < 0, а невозможности протекания реакции D rG 0> > 0. Если D rG 0 не сильно отличается от нуля в ту или другую сторону, то при протекании реакции наступает равновесие системы, при котором в системе будут находиться как исходные вещества, так и продукты. Причем, чем меньше D rG 0 (D rG 0→ − ∞), тем меньше при равновесии будет исходных веществ и больше продуктов реакции. И наоборот, чем больше D rG 0 (D rG 0→ +∞), тем больше при равновесии будет исходных веществ и меньше продуктов. Изохорно-изотермический процесс (V –const, Т –const). В изохорном процессе d QV = dU, следовательно, неравенство, определяющее условие его самопроизвольного протекания, приобретает вид dU – T × dS £ 0. При постоянной температуре: d (U – T × S)£ 0. Выражение под знаком дифференциала заменяется функцией A º U – T × S. A – функция состояния системы, получившая название энергия Гельмгольца. Очевидно, что условием самопроизвольного протекания изохорно-изотермического процесса будет dА < 0 (D А < 0), а условием равновесия – dА =0 (D А =0). Применение энергии Гельмгольца для определения направления протекания изохорно-изотермических процессов аналогично применению энергии Гиббса для изобарно-изотермических процессов. Изоэнтропные процессы (S –const). Поскольку условием самопроизвольного протекания процесса и равновесия в термодинамических системах является dU + p× dV – T× dS £ 0, то в процессах, идущих при постоянном объеме, оно преобразуется в dU £ 0(D U £ 0), а в процессах при постоянном давлении – в dН £ 0(D Н £ 0).
|

 . Условие состояния термодинамического равновесия системы
. Условие состояния термодинамического равновесия системы  .
. . Это условие может быть распространено и на замкнутые системы, в которых происходит обмен энергией с окружающей средой. В этом случае, согласно первому началу термодинамики: d Q = dU + p × dV, термодинамическим условием самопроизвольного протекания процесса будет dU+p × dV – T × dS < 0, а условиемсостояния равновесия системы dU+pdV – T × dS =0. В общем виде это условие записывается как dU + p × dV – T × dS £ 0.
. Это условие может быть распространено и на замкнутые системы, в которых происходит обмен энергией с окружающей средой. В этом случае, согласно первому началу термодинамики: d Q = dU + p × dV, термодинамическим условием самопроизвольного протекания процесса будет dU+p × dV – T × dS < 0, а условиемсостояния равновесия системы dU+pdV – T × dS =0. В общем виде это условие записывается как dU + p × dV – T × dS £ 0. прямой реакции (слева направо) равно
прямой реакции (слева направо) равно  обратной реакции (справа налево) по величине и противоположно по знаку:
обратной реакции (справа налево) по величине и противоположно по знаку:  .
. .
. ;
; .Поскольку
.Поскольку 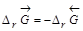 , то обратная реакция по отношению к окислению возможна, если D rG 0(Т)»D rН 0 – Т× D rS 0> 0, что выполняется при температуре выше
, то обратная реакция по отношению к окислению возможна, если D rG 0(Т)»D rН 0 – Т× D rS 0> 0, что выполняется при температуре выше  = 840, 47 К.
= 840, 47 К.


