Второе начало термодинамики
Анализ работы идеальной тепловой машины по циклу Карно, показал, что коэффициент полезного действия h, не зависит от природы рабочего тела, а определяется только температурным интервалом, в котором совершается работа (теорема Карно-Клаузиуса) (Carnot; Clausius):
где Q 1 – количество теплоты, сообщенное рабочему телу при температуре T 1; Q 2 – количество теплоты, отданное рабочим телом при температуре T 2. Если представить цикл Карно суммой бесконечно малых циклов, в каждом из которых Для обратимого (равновесного) процесса изменение энтропии равно:
Для необратимого (неравновесного) процесса, как было показано на примере расширения идеального газа, работа, производимая системой в самопроизвольном процессе, меньше работы, производимой в равновесном процессе: W неравн< W равн. Принимая во внимание первое начало термодинамики dU =d Q + d W и учитывая, что внутренняя энергия – функция состояния (dU равн= dU неравн), получаем, что d Q неравн > d Q равн. Соответственно для необратимого (неравновесного) процесса изменение энтропии В общем случае для любого процесса можно написать:
знак равенства относится к равновесным процессам, знак неравенства – к неравновесным. Согласно первому началу термодинамики d Q = dU + p × dV, следовательно, T× dS ³ dU + p × dV. В изолированной системе dU = dV =0, а так как Т > 0, то dS ³ 0. Второе начало термодинамики утверждает, что в изолированной системе самопроизвольно протекают процессы с увеличением энтропии, которые прекращаются при достижении ее максимального значения, соответствующего состоянию термодинамического равновесия. Энтропия играет большую роль во всех процессах в природе, в частности является одним из факторов, определяющих направление самопроизвольного протекания химических реакций и достижения равновесия в системах.
|

 или
или  ,
, , то в циклическом процессе
, то в циклическом процессе 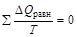 , а это значит, что интеграл, взятый по замкнутому контуру, равен нулю:
, а это значит, что интеграл, взятый по замкнутому контуру, равен нулю:  . Следовательно, подынтегральная функция
. Следовательно, подынтегральная функция  является функцией состояния. Эту функцию Клаузиус назвал энтропией (S) (entropia — превращение).
является функцией состояния. Эту функцию Клаузиус назвал энтропией (S) (entropia — превращение). ,
,  .
. .
.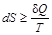 ,
,  ;
;


