В справочном пособии приведены фармацевтические данные, фармакокинетика, фармакодинамика, показания и способы применения более 700 препаратов, применяемых в практике ветеринарной медицины.
МАТЕМАТИКА
МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ
для студентов факультета непрерывного
профессионального образования
(для профилей: Технические системы в агробизнесе,
Электрооборудование и электротехнологии,
Энергообеспечение предприятий,
Технология продукции и организация общественного питания)
Составители:
к.ф.м.н., доц. Карпова В.С.,
к.ф.м.н., доц. Хохряков Н.В.,
к.ф.м.н., доц. Юберев Н.Н.
Ижевск 2012
ПРЕДИСЛОВИЕ
Настоящие методические материалы предназначены для студентов-заочников инженерно-технических специальностей, обучающихся на факультете непрерывного профессионального образования ФГБОУ ВПО «Ижевская ГСХА».
Методические материалы содержат задания для двух контрольных работ, которые составлены по двадцативариантной системе. В них также приводится подробное решение каждого типа задач, включенных в контрольные работы.
ТАБЛИЦЫ ВАРИАНТОВ
Студент выполняет тот вариант контрольной работы, который совпадает с последней цифрой его учебного шифра и соответствует его специальности. При этом, если предпоследняя цифра учебного шифра есть число нечетное (то есть 1, 3, 5, 7, 9), то номера задач для соответствующего варианта даны в таблице 1 (профиль ТСА, ТПООП) и в таблице 3 (профили ЭОЭТ и ЭОП). Если же предпоследняя цифра учебного шифра есть число четное или нуль (то есть 2, 4, 6, 8, 0), то номера задач для соответствующего варианта даны в таблице 2 (профиль ТСА, ТПООП) и в таблице 4 (профили ЭОЭТ и ЭОП).
Профиль ТСА, ТПООП
Таблица 1
| Вариант
| Контрольная работа №1
| Контрольная работа №2
|
|
| 1.1; 2.1; 3.1; 4.1; 5.1; 6.1
| 7.1; 8.1; 10.1; 11; 12.1(а); 13.1; 14.1
|
|
| 1.2; 2.2; 3.2; 4.2; 5.2; 6.2
| 7.2; 8.2; 10.2; 11; 12.2(а); 13.2; 14.2
|
|
| 1.3; 2.3; 3.3; 4.3; 5.3; 6.3
| 7.3; 8.3; 10.3; 11; 12.3(а); 13.3; 14..3
|
|
| 1.4; 2.4; 3.4; 4.4; 5.4; 6.4
| 7.4; 8.4; 10.4; 11; 12.4(а); 13.4; 14.4
|
|
| 1.5; 2.5; 3.5; 4.5; 5.5; 6.5
| 7.5; 8.5; 10.5; 11; 12.5(а); 13.5; 14.5
|
|
| 1.6; 2.6; 3.6; 4.6; 5.6; 6.6
| 7.6; 8.6; 10.6; 11; 12.6(а); 13.6; 14.6
|
|
| 1.7; 2.7; 3.7; 4.7; 5.7; 6.7
| 7.7; 8.7; 10.7; 11; 12.7(а); 13.7; 14.7
|
|
| 1.8; 2.8; 3.8; 4.8; 5.8; 6.8
| 7.8; 8.8; 10.8; 11; 12.8(а); 13.8; 14.8
|
|
| 1.9; 2.9; 3.9; 4.9; 5.9; 6.9
| 7.9; 8.9; 10.9; 11; 12.9(а); 13.9; 14.9
|
|
| 1.10; 2.10; 3.10; 4.10; 5.10; 6.10
| 7.10; 8.10; 10.10; 11; 12.10(а); 13.10; 14.10
|
Профиль ТСА, ТПООП
Таблица 2
| Вариант
| Контрольная работа №1
| Контрольная работа №2
|
|
| 1.11; 2.11; 3.11; 4.11; 5.11; 6.11
| 7.11; 8.11; 10.11; 11; 12.11(а); 13.11; 14.11
|
|
| 1.12; 2.12; 3.12; 4.12; 5.12; 6.12
| 7.12; 8.12; 10.12; 11; 12.12(а); 13.12; 14.12
|
|
| 1.13; 2.13; 3.13; 4.13; 5.13; 6.13
| 7.13; 8.13; 10.13; 11; 12.13(а); 13.13; 14.13
|
|
| 1.14; 2.14; 3.14; 4.14; 5.14; 6.14
| 7.14; 8.14; 10.14; 11; 12.14а); 13.14; 14.14
|
|
| 1.15; 2.15; 3.15; 4.15; 5.15; 6.15
| 7.15; 8.15; 10.15; 11; 12.15(а); 13.15; 14.15
|
|
| 1.16; 2.16; 3.16; 4.16; 5.16; 6.16
| 7.16; 8.16; 10.16; 11; 12.16(а); 13.1; 6 14.16
|
|
| 1.17; 2.17; 3.17; 4.17; 5.17; 6.17
| 7.17; 8.17; 10.17; 11; 12.17(а); 13.17; 14.17
|
|
| 1.18; 2.18; 3.18; 4.18; 5.18; 6.18
| 7.18; 8.18; 10.18; 11; 12.18(а); 13.18; 14.18
|
|
| 1.19; 2.19; 3.19; 4.19; 5.19; 6.19
| 7.19; 8.19; 10.19; 11; 12.19(а); 13.19; 14.19
|
|
| 1.20; 2.20; 3.20; 4.20; 5.20; 6.20
| 7.20; 8.20; 10.20; 11; 12.20(а); 13.20; 14.20
|
Профили ЭОЭТ и ЭОП
Таблица 3
| Вари-ант
| Контрольная работа №1
| Контрольная работа №2
|
|
| 1.1; 2.1; 3.1; 4.1; 5.1; 6.1
| 7.1; 9.1; 10.1; 11; 12.1(б); 13.1; 14.1
|
|
| 1.2; 2.2; 3.2; 4.2; 5.2; 6.2
| 7.2; 9.2; 10.2; 11; 12.2(б); 13.2; 14.2
|
|
| 1.3; 2.3; 3.3; 4.3; 5.3; 6.3
| 7.3; 9.3; 10.3; 11; 12.3(б); 13.3; 14..3
|
|
| 1.4; 2.4; 3.4; 4.4; 5.4; 6.4
| 7.4; 9.4; 10.4; 11; 12.4(б); 13.4; 14.4
|
|
| 1.5; 2.5; 3.5; 4.5; 5.5; 6.5
| 7.5; 9.5; 10.5; 11; 12.5(б); 13.5; 14.5
|
|
| 1.6; 2.6; 3.6; 4.6; 5.6; 6.6
| 7.6; 9.6; 10.6; 11; 12.6(б); 13.6; 14.6
|
|
| 1.7; 2.7; 3.7; 4.7; 5.7; 6.7
| 7.7; 9.7; 10.7; 11; 12.7(б); 13.7; 14.7
|
|
| 1.8; 2.8; 3.8; 4.8; 5.8; 6.8
| 7.8; 9.8; 10.8; 11; 12.8(б); 13.8; 14.8
|
|
| 1.9; 2.9; 3.9; 4.9; 5.9; 6.9
| 7.9; 9.9; 10.9; 11; 12.9(б); 13.9; 14.9
|
|
| 1.10; 2.10; 3.10; 4.10; 5.10; 6.10
| 7.10; 9.10; 10.10; 11; 12.10(б); 13.10; 14.10
|
Профили ЭОЭТ и ЭОП
Таблица 4
| Вари-ант
| Контрольная работа №1
| Контрольная работа №2
|
|
| 1.11; 2.11; 3.11; 4.11; 5.11; 6.11
| 7.11; 9.11; 10.11; 11; 12.11(б); 13.11; 14.11
|
|
| 1.12; 2.12; 3.12; 4.12; 5.12; 6.12
| 7.12; 9.12; 10.12; 11; 12.12(б); 13.12; 14.12
|
|
| 1.13; 2.13; 3.13; 4.13; 5.13; 6.13
| 7.13; 9.13; 10.13; 11; 12.13(б); 13.13; 14.13
|
|
| 1.14; 2.14; 3.14; 4.14; 5.14; 6.14
| 7.14; 9.14; 10.14; 11; 12.14(б); 13.14; 14.14
|
|
| 1.15; 2.15; 3.15; 4.15; 5.15; 6.15
| 7.15; 9.15; 10.15; 11; 12.15(б); 13.15; 14.15
|
|
| 1.16; 2.16; 3.16; 4.16; 5.16; 6.16
| 7.16; 9.16; 10.16; 11; 12.16(б); 13.1; 6 14.16
|
|
| 1.17; 2.17; 3.17; 4.17; 5.17; 6.17
| 7.17; 9.17; 10.17; 11; 12.17(б); 13.17; 14.17
|
|
| 1.18; 2.18; 3.18; 4.18; 5.18; 6.18
| 7.18; 9.18; 10.18; 11; 12.18(б); 13.18; 14.18
|
|
| 1.19; 2.19; 3.19; 4.19; 5.19; 6.19
| 7.19; 9.19; 10.19; 11; 12.19(б); 13.19; 14.19
|
|
| 1.20; 2.20; 3.20; 4.20; 5.20; 6.20
| 7.20; 9.20; 10.20; 11; 12.20(б); 13.20; 14.20
|
ЗАДАНИЯ ДЛЯ КОНТРОЛЬНЫХ РАБОТ
КОНТРОЛЬНАЯ РАБОТА №1
1. Решить систему линейных уравнений методом Гаусса.
1.1.  1.2.
1.2. 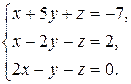
1.3.  1.4.
1.4. 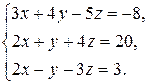
1.5.  1.6.
1.6. 
17.  1.8.
1.8. 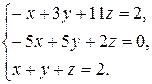
19.  1.10.
1.10. 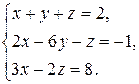
1.11. 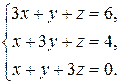 1. 12.
1. 12. 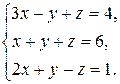
1.13.  1.14.
1.14. 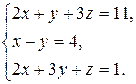
1.15.  1.16.
1.16. 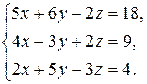
1.17.  1.18.
1.18. 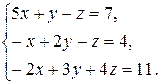
1.19.  1.20.
1.20. 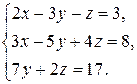
2. Определить тип кривой, найти ее параметры; определить угловой коэффициент прямой. Найти точки пересечения данных линий и сделать чертеж.
2.1.  ;
;  .
.
2.2.  ;
;  .
.
2.3. 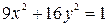 ;
;  .
.
2.4.  ;
;  .
.
2.5.  ;
;  .
.
2.6.  ;
;  .
.
2.7.  ;
;  .
.
2.8.  ;
;  .
.
2.9.  ;
;  .
.
2.10.  ;
;  .
.
2.11.  ;
;  .
.
2.12.  ;
;  .
.
2.13.  ;
;  .
.
2.14.  ;
;  .
.
2.15.  ;
;  .
.
2.16.  ;
;  .
.
2.17.  ;
;  .
.
2.18.  ;
;  .
.
2.19.  ;
;  .
.
2.20.  ;
;  .
.
3. Даны координаты вершин пирамиды АВСD. Требуется:
1) записать векторы  в системе орт
в системе орт  и найти модули этих векторов;
и найти модули этих векторов;
2) найти угол между векторами  и
и  ;
;
3) найти проекцию вектора  на вектор
на вектор  ;
;
4) найти площадь грани АВС;
5) найти объем пирамиды АВСD;
6) составить уравнение ребра АС;
7) составить уравнение грани АВС.
3.1. 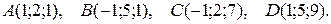
3.2. 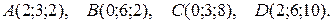
3.3. 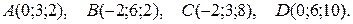
3.4. 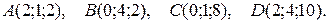
3.5. 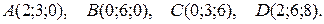
3.6. 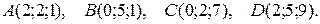
3.7. 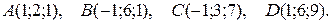
3.8. 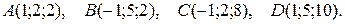
3.9. 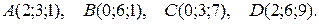
3.10. 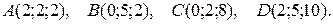
3.11. 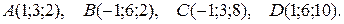
3.12. 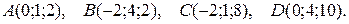
3.13. 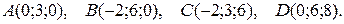
3.14. 
3.15. 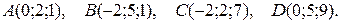
3.16. 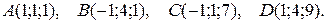
3.17. 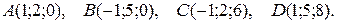
3.18. 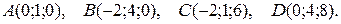
3.19. 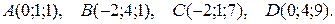
3.20. 
4. Провести полное исследование функции методами дифференциального исчисления и построить ее график.
41.  . 4.2.
. 4.2.  .
.
4.3.  . 4.4.
. 4.4.  .
.
4.5.  . 4.6.
. 4.6.  .
.
4.7.  . 4.8.
. 4.8.  .
.
4.9.  . 4.10.
. 4.10.  .
.
4.11.  . 4.12.
. 4.12.  .
.
4.13.  . 4.14.
. 4.14.  .
.
4.15.  . 4.16.
. 4.16.  .
.
4.17.  . 4.18.
. 4.18.  .
.
4.19. 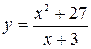 . 4.20.
. 4.20.  .
.
5. Решить систему двух линейных уравнений в области комплексных чисел по формулам Крамера. Найденные 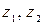 изобразить на комплексной плоскости в виде векторов и записать их в показательной и тригонометрической формах.
изобразить на комплексной плоскости в виде векторов и записать их в показательной и тригонометрической формах.
5.1.  5.2.
5.2. 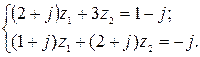
5.3.  5.4.
5.4. 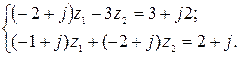
5.5.  5.6.
5.6. 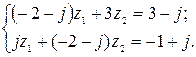
5.7.  5.8.
5.8. 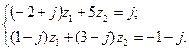
5.9.  5.10.
5.10. 
5.11.  5.12.
5.12. 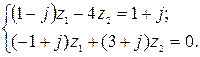
5.13.  5.14.
5.14. 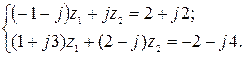
5.15. 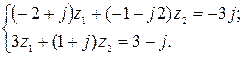 5.16.
5.16. 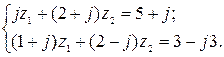
5.17.  5.18.
5.18. 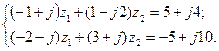
5.19.  5.20.
5.20. 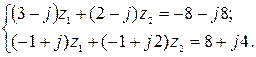
6. а) Вычислить площадь фигуры, расположенной в первом квадранте и ограниченной параболой, прямой и осью Ox.
б) Найти объем тела, образованного вращением этой фигуры вокруг оси Ох.
6.1.  .
.
6.2.  .
.
6.3.  .
.
6.4.  .
.
6.5.  .
.
6.6  .
.
6.7.  .
.
6.8.  .
.
6.9.  .
.
6.10.  .
.
6.11 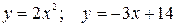 .
.
6.12.  .
.
6.13  .
.
6.14.  .
.
6.15.  .
.
6.16  .
.
6.17  .
.
6.18.  .
.
6.19.  .
.
6.20.  .
.

 1.2.
1.2. 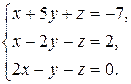
 1.4.
1.4. 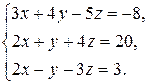
 1.6.
1.6. 
 1.8.
1.8. 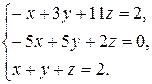
 1.10.
1.10. 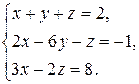
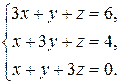 1. 12.
1. 12. 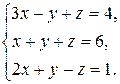
 1.14.
1.14. 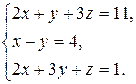
 1.16.
1.16. 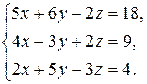
 1.18.
1.18. 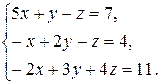
 1.20.
1.20. 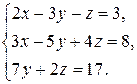
 ;
;  .
. ;
;  .
.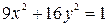 ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. в системе орт
в системе орт  и найти модули этих векторов;
и найти модули этих векторов; и
и  ;
; на вектор
на вектор  ;
;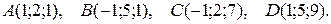
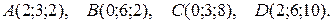
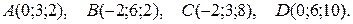
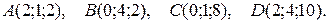
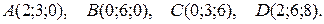
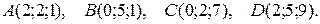
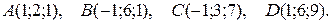
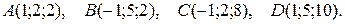
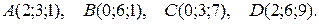
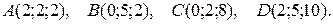
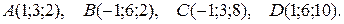
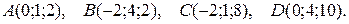
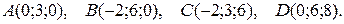

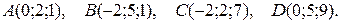
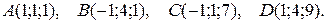
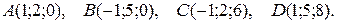
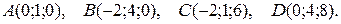
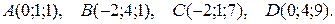

 . 4.2.
. 4.2.  .
. . 4.4.
. 4.4.  .
. . 4.6.
. 4.6.  .
. . 4.8.
. 4.8.  .
. . 4.10.
. 4.10.  .
. . 4.12.
. 4.12.  .
. . 4.14.
. 4.14.  .
. . 4.16.
. 4.16.  .
. . 4.18.
. 4.18.  .
.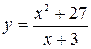 . 4.20.
. 4.20.  .
.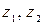 изобразить на комплексной плоскости в виде векторов и записать их в показательной и тригонометрической формах.
изобразить на комплексной плоскости в виде векторов и записать их в показательной и тригонометрической формах. 5.2.
5.2. 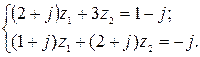
 5.4.
5.4. 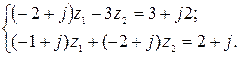
 5.6.
5.6. 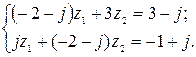
 5.8.
5.8. 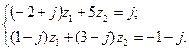
 5.10.
5.10. 
 5.12.
5.12. 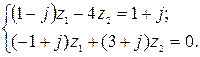
 5.14.
5.14. 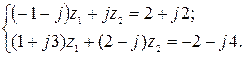
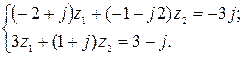 5.16.
5.16. 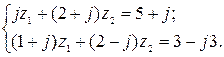
 5.18.
5.18. 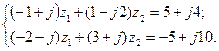
 5.20.
5.20. 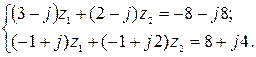
 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.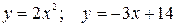 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.


